汽车运行的工况很复杂,需要仿真的问题无穷无尽:操稳,平顺,NVH…无数种工况都需要进行处理。于是,轮胎动力学就成为了一门永远都不会有标准答案的学问——而这只有一个原因——轮胎是汽车与路面接触的唯一部件,汽车的动力来源就是取自轮胎。
所以,安部正人直接把轮胎力学作为车辆运动力学控制理论开篇的第一章,排在了车辆动力学基础之前,足见这门学问的分量。
如果你喜欢数学,觉得数学学不够,那就来研究轮胎力学吧!总有一天,你会体验到自己的学习极限并感到深深的绝望!
达芬奇说:力学是数学的天堂,有什么样的数学,就有什么样的力学。
牛顿说:几何学建立在力学实践之上,它无非是普通力学的一部分。
轮胎力学,这不是一门夕阳学问,MF,Unitire…目前全世界都没有一个非常完美的轮胎理论能够解决目前轮胎建模中遇到的所有问题,这里仍然充满了挑战,挑战永无止境。
壹
地面上行驶的车辆,从其运动形式可以大致分为以下两种:
-
一种是完全被预先设置在地面上的轨道所束缚而行驶,以铁路车辆为代表。
-
另一种是不受轨道等限制,可以在地面上通过车轮的操舵(掌舵操作)自由行驶的车辆:飞机可以在大气中不受其他限制的情况下自由飞行,船舶在水面上同样可以通过舵的操作自由航行。
飞机、船舶,以及能够在地面上通过车轮的操舵自由行驶的车辆,都不必拘泥于预先规定的轨道等,可以在自己的意识下自由地在空间或平面内进行运动。
从运动力学的角度来看,飞机、船舶、汽车这三个运动体都可以说是具有相当本质的共性,即接受由自己的运动产生的力,利用这种力进行自己希望的运动。
更具体地说,飞机翅膀和大气的相对运动带来升力,船舶船体和水的相对运动产生升力,车辆根据车辆和地面的相对运动,车轮上工作受力,并自由运动,发挥其功能。
如上所述,上述三者的运动体的运动和控制是与运动体的本质功能有关的问题,关于飞机作为航空(运动)力学,关于船舶作为船体运动力学被体系化。我们今后也可以把运动和控制作为问题的车辆,看作和飞机和船舶一样,通过自己的运动自己制造力,在地上自由地进行独立运动的对象来处理。
为了处理这样的车辆运动和控制问题,这里就要试设想一下典型的车辆的运动动力学模型:
这个模型是操纵前方2轮和后方2轮的车轮被安装在看做是刚体的车身上的车辆——可以安装车轮,从而不直接沿着轨道而能自由行驶的车辆。除了一般最熟悉的乘用车、大型卡车、公共汽车等之外,还有建设用车辆、产业用车辆等特殊车辆。
乍一看来,似乎不能直接讨论这些运动。但是。如果以这些车辆的基本运行为主题的话。通过将车辆抽象化到最一般、最简单的四轮车当中来思考,可以获得很多基本的车辆运动知识。
在上述的车辆动力学模型中,车轮不具有重量,被认为是刚性的车身代表车辆的重量。现在,假设以该车辆的重心点为原点,为车辆建立坐标系,车辆的前后方向是x轴,上下方向z轴,左右方向为y轴。
有了这个坐标为基准,就可以将车辆运动的自由度作为三维空间内刚体的运动分类为以下6种。
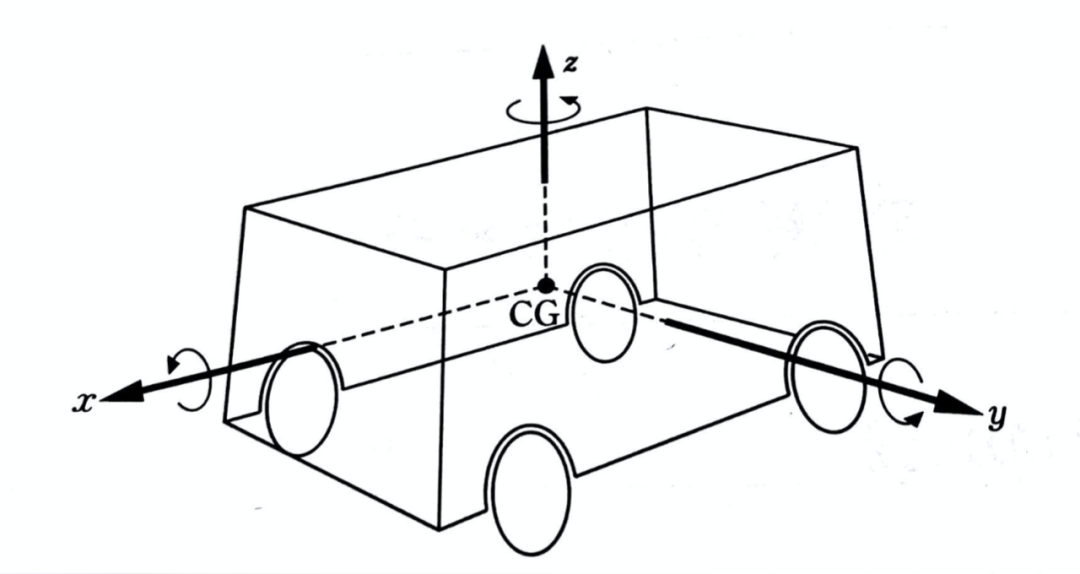
① z方向的平移,上下运动(Up & Down)
② y方向的平移,左右运动(Lateral)
③ x方向的平移,前后运动(longitudinal)
④ x轴的旋转运动(Rolling)
⑤ y轴的旋转运动(Pitching)
⑥ z轴的旋转运动(Yawing)
再进一步,把六项运动分为两部分加以考虑:
一种是.①、③、⑤的运动,这些是与操舵没有任何直接关系:
-
①的运动具体来说是由于路面不平而产生的上下方向运动,与行驶中车辆的乘坐感觉有关。
-
③的运动是前后方向的直线运动,包括油门和刹车的车辆驱动和制动。
-
⑤是伴随着上下方向的路面不齐和③的运动而产生的运动,这也与车辆的乘坐舒适度有关。
与此相对,②、④、⑥是另外一类与操舵相关的:
-
②的运动是通过操舵来进行的车辆横向运动
-
⑥的运动是通过操舵来改变车辆方向的运动
-
④的运动伴随着②和⑥的运动而产生的车辆滚动。
通常的车辆由车上的驾驶员控制其运动。根据驾驶员的操舵,车辆按照自己的运动力学的固有特性,横向运动,围绕垂直z轴的Yawing运动,并伴随着这个,车身进行滚动运动。
司机并不是完全没有意义的操舵。司机可以看到前方道路,了解行驶目标路线的情况,或者在道路前方设定自己应该走的目标路线。与此同时,司机需要判断自己对照目标路线处于怎样的位置,基于这些信息,驾驶员自行判断是否进行适当的操舵,从而让车辆按照指定的目标路线或驾驶员自己设定的目标路线运动。
下图展示了这样的车辆运动与控制之间的关系。
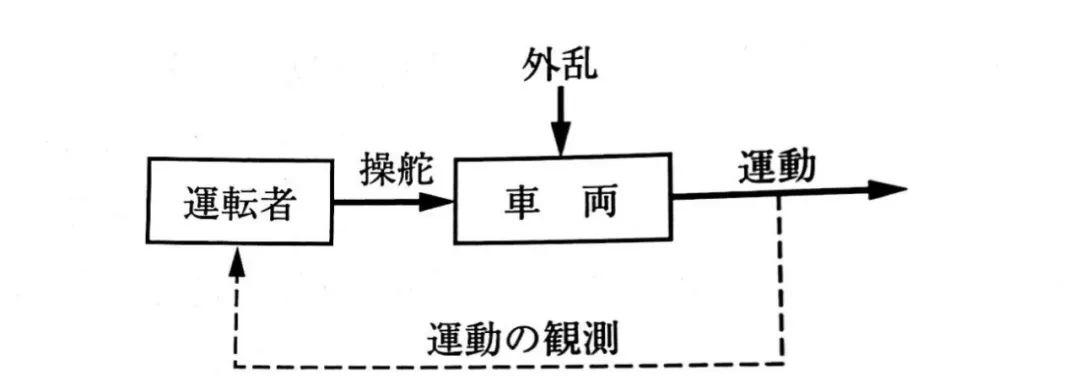
这样,不受地面上设定的轨道等直接的约束的影响,通过操舵在平面内自由运动的车辆,通过人或其他方法受到适当的控制,得以进行有意义的运动。我们的兴趣的中心和研究对象就更加明确了:
-
通过观察车辆对某一特定的操舵的运动的反应,而明确的车辆本身就具有的独特的运动力学性质。
-
具有某种运动力学性质的车辆,在通过人或其他方法得到控制的情况下,会达成怎样的运动。
-
如果是受人控制的车辆,怎样的具有运动力学性的车辆对控制者来说容易控制。
这些问题将是本文所研究的重点。
贰
在前一节中我们谈到,车辆运动不直接拘泥于预先放置在地上的轨道,可以在自己的意志下,自由独立于水平面内运动。并且,车辆运动的力是由车辆对地面相对运动产生的。
车辆和地面的接触点是车轮。车轮如果在与旋转面成直角的方向上具有速度分量,则会受到垂直于其行驶方向的作用力。
也就是说,上述使车辆运动成为可能的力量是指,通过车辆和地面的相对运动,车轮从地面受到的力——这正好对应于在飞机运动中垂直于机翼行进方向工作的升力和在船体转向时,垂直传锑运动方向的浮力(对船体来说是侧向的力)。
这样,作为对象处理的车辆所安装的车轮,不仅承担着支撑着车身一边转动,对地面前后方向产生驱动和制动力的作用,还承担着使这种车辆的本质功能即自立运动成为可能的作用。
因此,要处理车辆的运动和控制问题,就必须事先掌握使其运动和控制成为可能的、关于在车轮上工作的能力的知识。由此,本章主要阐明了车轮和地面相对运动产生的力的产生机制及其力的性质——这便是轮胎力学。
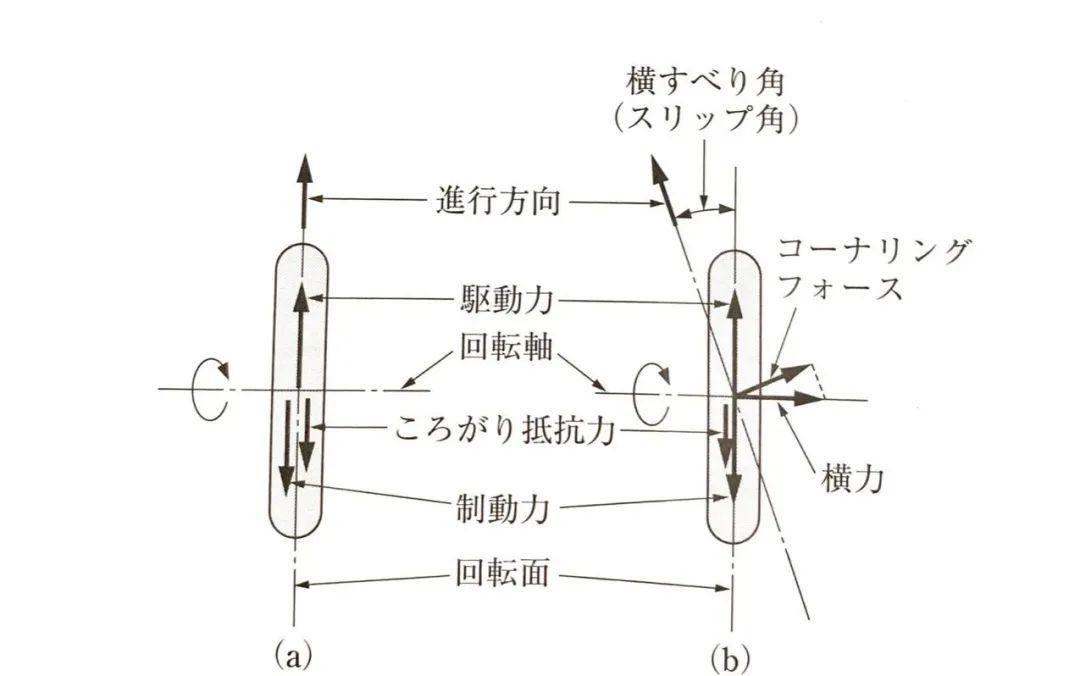
当车辆直线行驶时,车轮的行驶方向通常位于旋转平面内。车轮的旋转平面与其行驶方向时一致的(图a所示)。当车辆横摆或转弯时,车轮的行驶方向就会跑出其旋转平面(图b所示)。
图b是发生侧滑的情况,车轮旋转平面的垂直方向将产生力——这可以看作是车轮发生侧向滑动时抵抗侧滑的反作用力——这是车辆实现独立运动所必须依赖的侧向力。
垂直于车轮行驶方向的分力被称为侧偏力,当侧偏角(slip angle,车轮行驶方向和车轮旋转平面之间的夹角)很小的时候,可以认为侧偏力和侧向力相同。
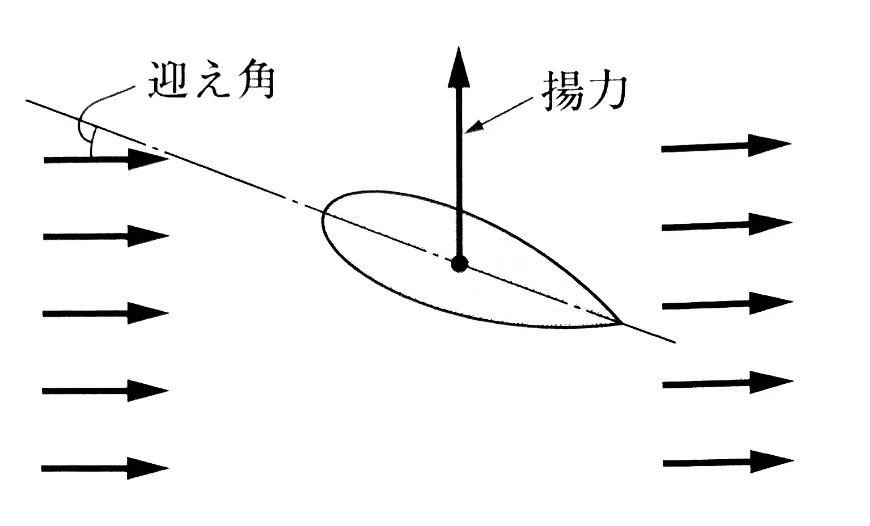
这种侧向力可以被看作是流体力学当中的概念:流体中以迎面角前进的物体受到的升力。
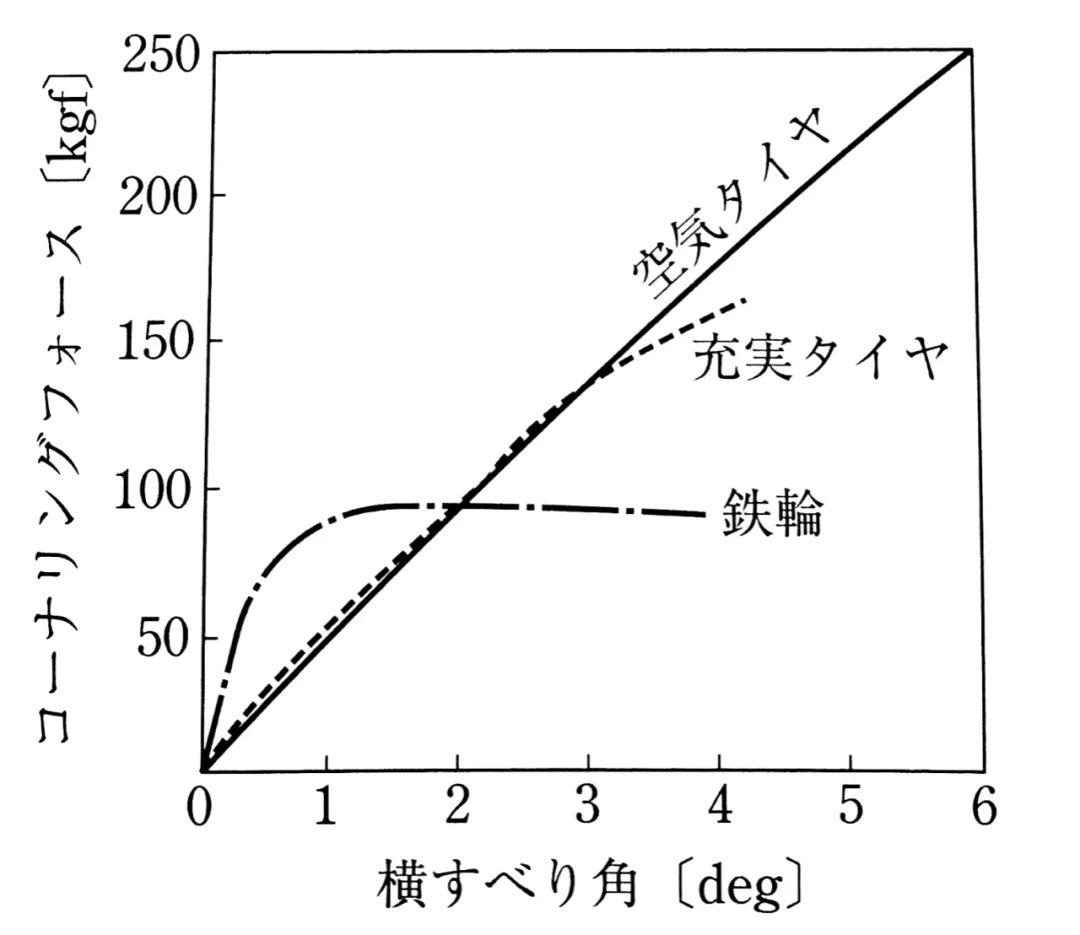
无论是哪种轮胎,在做伴有侧滑的转动时,都会产生垂直于车轮旋转面的力。上图对比了不同侧偏角的情况下,充气橡胶轮胎,实心橡胶轮胎,铁车轮产生的侧向力的差异。
很容易会发现,铁车轮所能产生的最大侧向力,还不到橡胶轮胎的1/3。而且,充气橡胶轮胎所能产生的侧向力要大于实心橡胶轮胎车轮,侧向力相对侧偏角也更加线性。
对于车辆独立运动,伴有侧滑的车轮能产生的侧向力越大越好。因此,可在无约束的平面上自由运动的车辆通常都装载充气轮胎——这不光有利于乘坐舒适性,而且还有利于获得操纵车辆所需的侧向力。
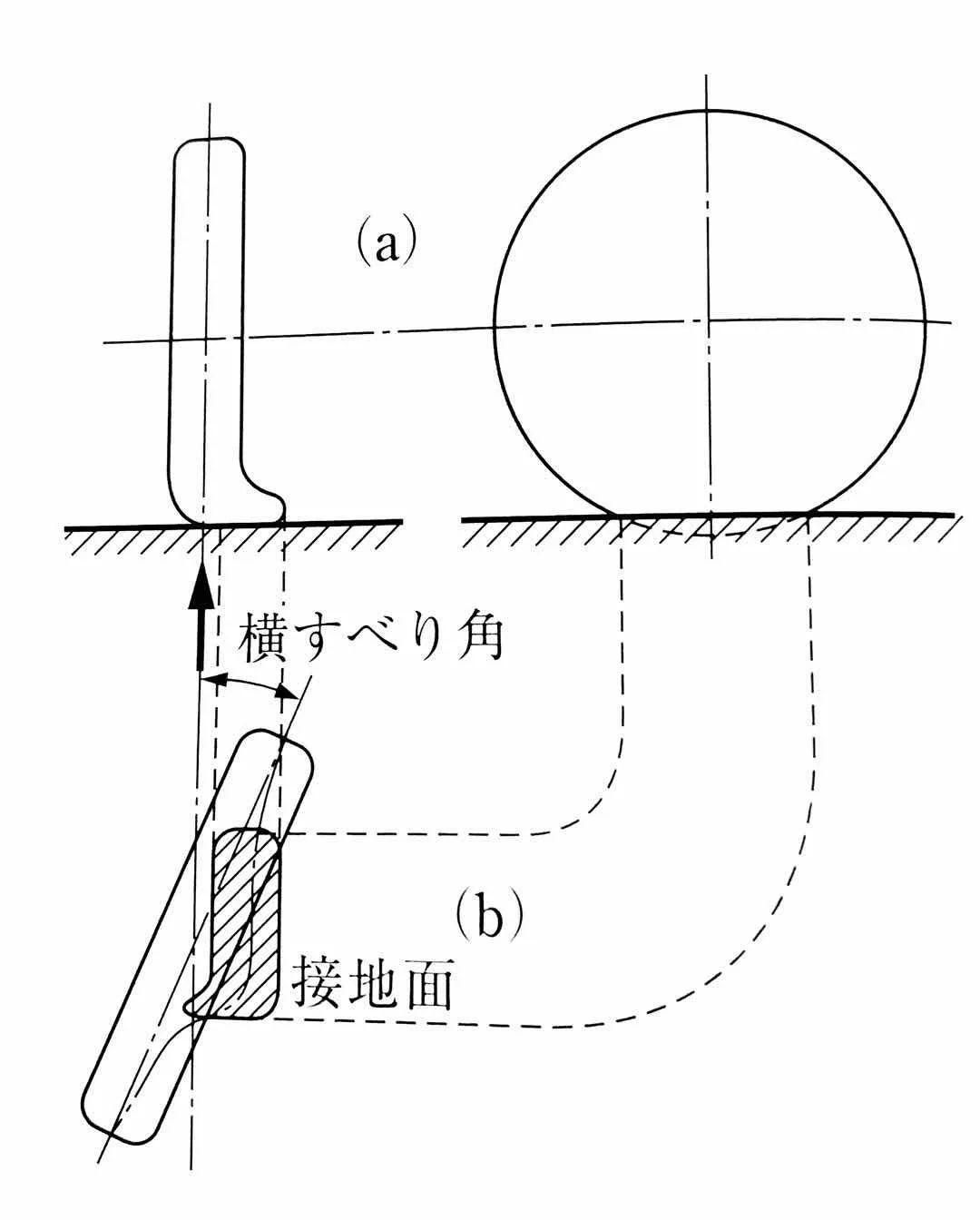
一般而言,轮胎与地面的接触产生力。上图显示了一个伴有侧向滑动的轮胎及其在工作状态下的变形。图a表示从轮胎的纵向和侧向观察到的轮胎变形,图b表示俯视观察到的轮胎接地区和外周的变形。
从轮胎接地区的前部看,轮胎变形的方向几乎与轮胎行驶的方向平行,在这一区域,轮胎和地面之间并未产生相对滑动。而轮胎的后端相对轮胎的行驶方向则产生了很大的侧向变形和相对滑动。
当侧偏角增大时:
轮胎接地区的前端仍然保持与轮胎行驶方向平行。
到了接地区中心,侧向变形在接地区的某点处达到最大。
此后,轮胎接地区滑离接地中心线,产生相对滑动,侧向变形不再增加。
如果侧偏角再进一步增加:
侧向变形的最大点会迅速地前移。
当轮胎的侧偏角达到10°-12°时:接地区将不再平行于轮胎行驶方向——而是前后部都产生与轮心几乎对称的变形。此时,可以认为接地区的所有位置都产生了与地面的相对滑动。
轮胎的侧向变形产生了一个作用于轮胎接地区的侧向力(lateral force),它的分布与轮胎变形的分布对应。在小侧偏角的情况下,轮胎的侧向力(垂直于车轮旋转方向)通常被看作是侧偏力(cornering force,垂直于车轮行驶方向)。
从轮胎的侧向变形来看,产生的侧向力的作用点并不一定与轮胎接地区的中心重合,因此会绕轮胎接地区的中心产生一个力矩,即所谓的”回正力矩“(self aligning torque)——其作用是使轮胎侧偏角减少。
于是,我们就引出了轮胎力学当中,真正重要的两个研究对象:
-
侧向力(lateral force)
-
回正力矩(self aligning torque)
侧向力和回正力矩特性可以被统一称作轮胎的侧偏特性。我们在下一节将详细讨论它。
值得一提的是,从悬挂几何的角度来讲,轮胎的侧向力可能不单单来自于轮胎的侧偏角,轮胎的外倾角(轮胎旋转平面与铅锤面之间的夹角)同样可以带来侧向力。
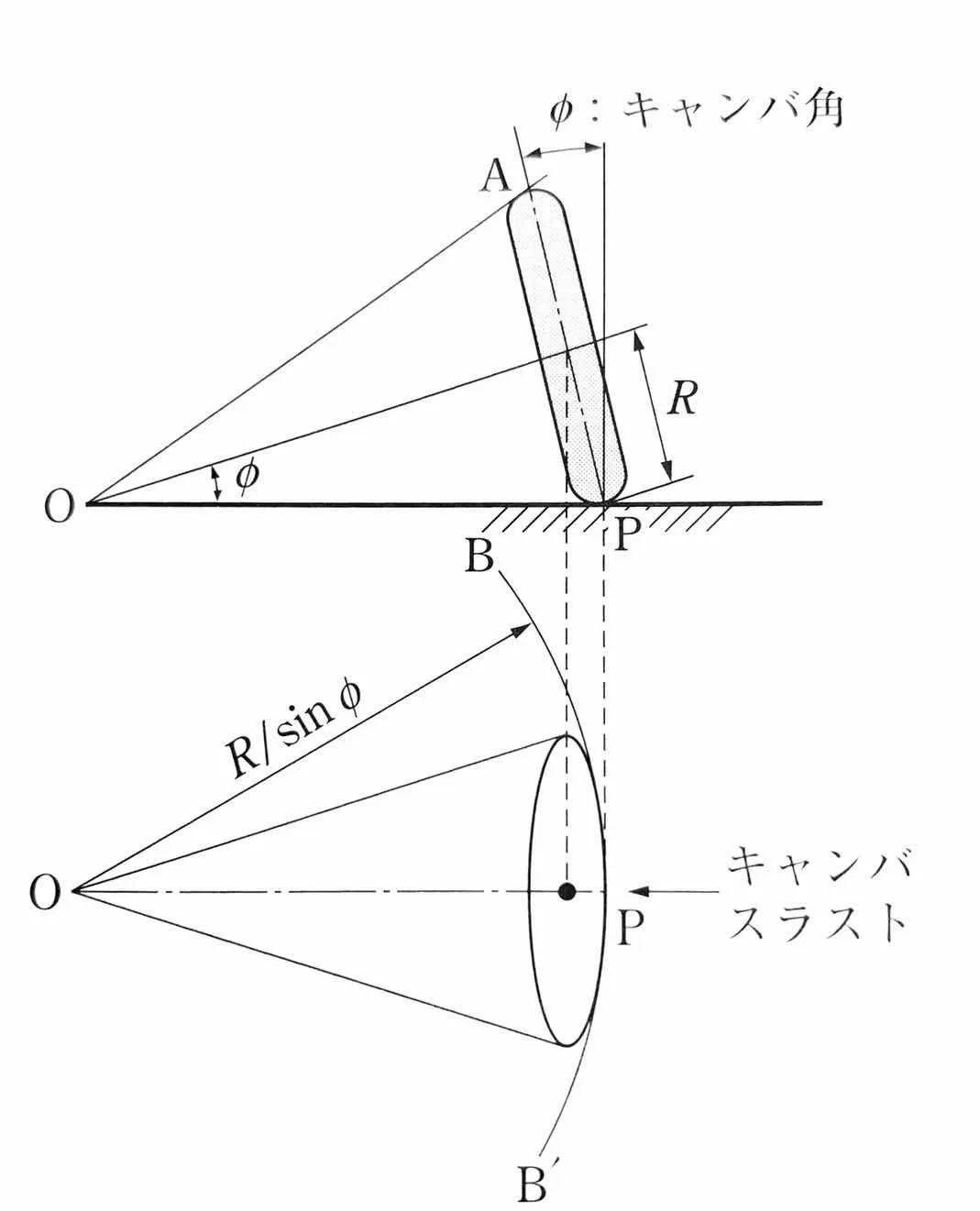
图:具有外倾角的轮胎带来的侧向力。
如果轮胎保持外倾角Φ(camber angle)不变,并在水平面内自由转动,则轨迹应该是半径为R/sinΦ的一段圆弧。如果轮胎被悬挂几何限制不能做这样的圆周运动,而是被限定只能做直线运动,则就会受到图示的力P的作用,这个由轮胎相对地面外倾而产生的侧向力被称作为外倾侧向力(camber thrust)。
叁
有关轮胎侧滑产生侧向力的分析中,Fiala所提出的数学模型广为流传,并通常被称作关于轮胎侧偏特性的Fiala理论。Fiala理论被看作是揭示轮胎侧偏特性的基本理论之一。
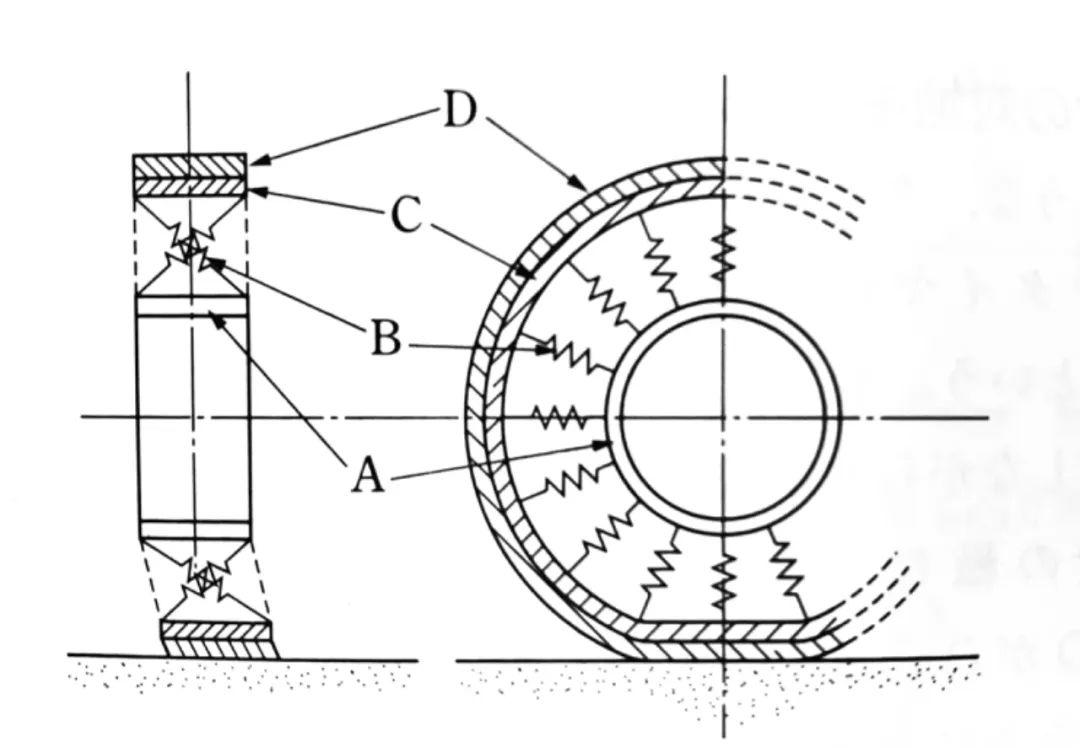
Fiala的轮胎结构模型如上图所示:
A,被看作刚体,相当于车轮的轮辋;
B,为等效弹簧,分别在径向和侧向等效替代可弹性变形的充气内胎和轮胎侧壁;
C,相当于较薄的轮胎胎面基底,并连接轮胎两边的侧壁;
D,相当于轮胎胎面橡胶,但它不是环状的连续体,而是由大量环绕轮胎周围的独立弹性体组成。
当侧向力作用于轮胎接地区时,轮胎将发生侧向变形。由于轮辋是刚体,不发生变形,而轮胎胎面基底则会产生侧向的弯曲(剪切)变形。
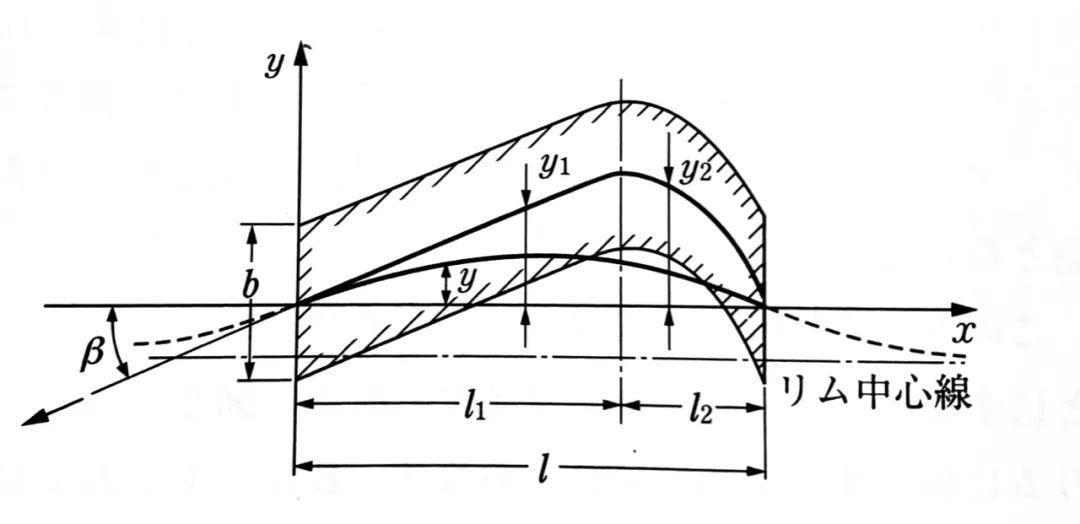
如图所示,x轴平行于轮辋中心线,y轴表示轮胎胎面基底偏离x轴的侧向位移。y1代表在0≤x≤L1范围内接地区中心线偏离x轴的侧向位移,y2表示在L1≤x≤L范围内接地区中心线偏离x轴的侧向位移。β为轮胎的侧偏角,L为接地区的长度,b为接地区的宽度。而且:
-
在L1范围内,轮胎与地面之间没有相对滑动
-
在L2范围(L1~L),轮胎与地面发生相对滑动
我们继续建模,来观察轮胎胎面基底的侧向变形y。
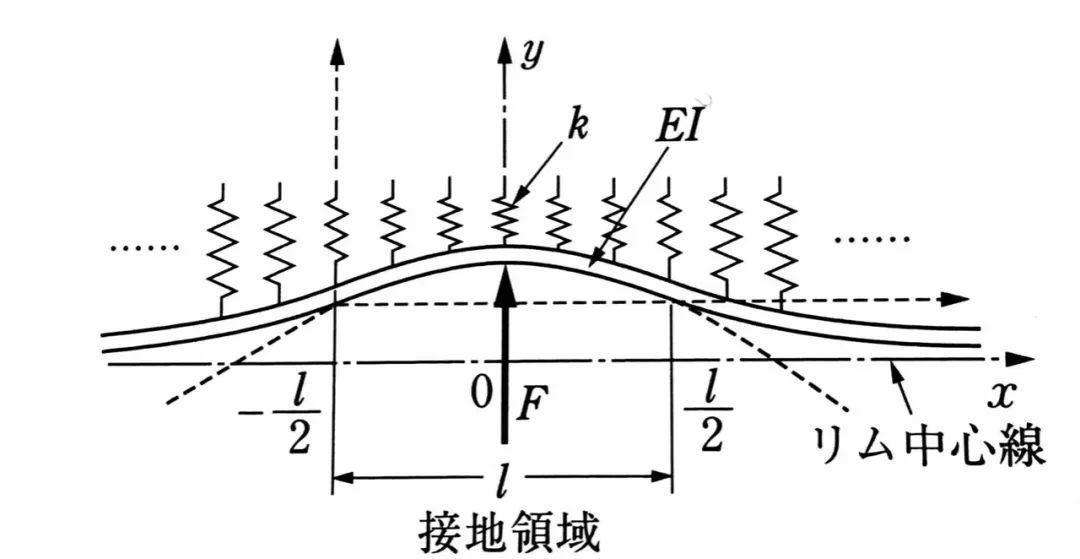
轮胎胎面基底沿着周向展开,就得到了以上图画,将圆变成一根梁来分析变型。这根梁放置在轮胎结构模型等效的弹簧上。如果轮胎受到的侧向力F仅沿y方向集中作用于x=0处,思考梁的变形可以得到以下方程:
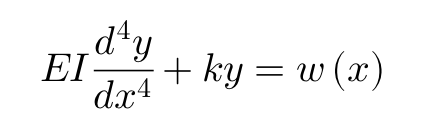
E为轮胎胎面材料的弹性模量,I为轮胎胎面基底的截面惯性(二次)矩,k为单位长度弹性基础的弹簧常数。
对公式求解,得到侧向位移的通用解为:
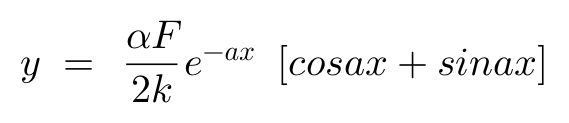 ,
,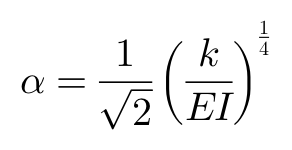
|ax|<< 1的情况下,Cosax ≈ 1,Sinax ≈ ax,上式可以简化为:
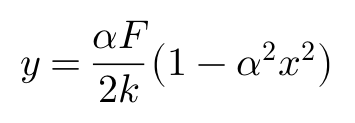
继续,移动原点位置,使y在x=0,x=L时为0,坐标变换后方程变为:
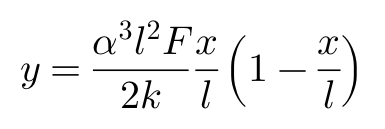
这个方程就是轮胎胎面基底侧向位移y的表达式。
胎面基底表达之外,我们还要看轮胎胎面橡胶真正的接地区域,即接地区中心线的侧向位移y1和y2。
y1的大小只与β相关:
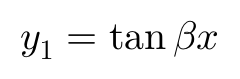
轮胎胎面橡胶与胎面基底之间产生了一个(y-y1)/d的剪切变形。
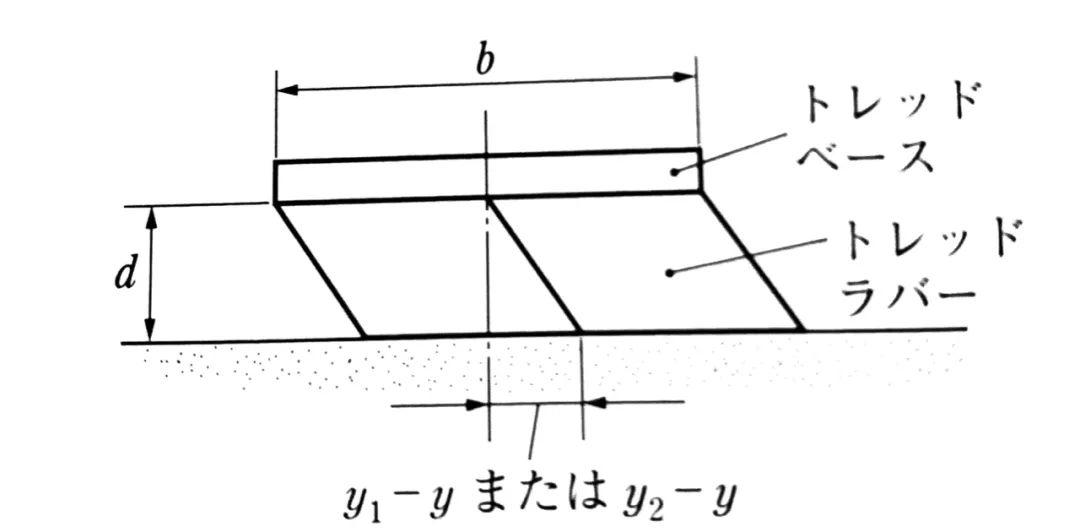
在接地区纵向各点,每单位长度作用有下式表达的侧向力:
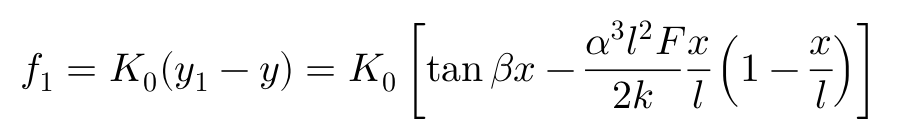
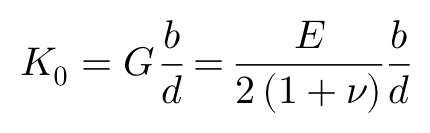
G代表轮胎胎面的剪切模量,ν代表泊松比。
随着接地区向后移动,y1-y将变大,f1也越来越大。如果f1的值超过地面与轮胎胎面橡胶之间的摩擦力,在L1~L(即L2)的范围内将产生相对滑动,胎面橡胶的剪切变形变为(y2-y)/d。
导致这一变形的力f2,即为轮胎胎面橡胶与地面之间的摩擦力。
为计算f2,我们设轮胎的垂直载荷为W,并假设W产生的接地区压力p沿x轴轴向的分布如下图所示:
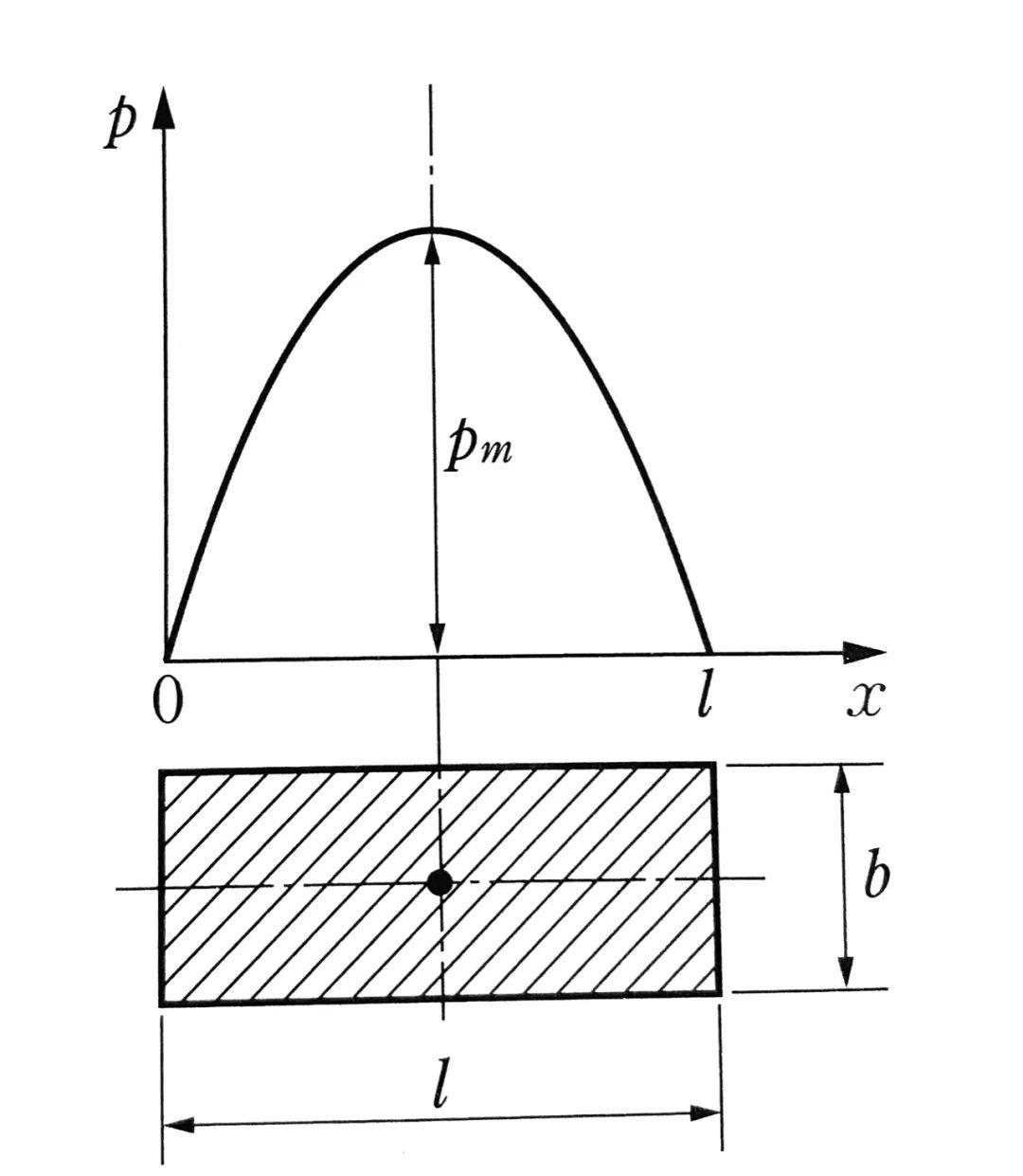
于是,载荷峰值位于轮胎接地区中心的方程可以表达为:
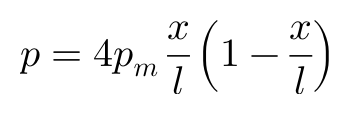 ,
,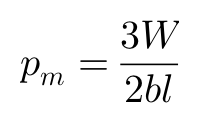
进而,f2的方程可以写为:
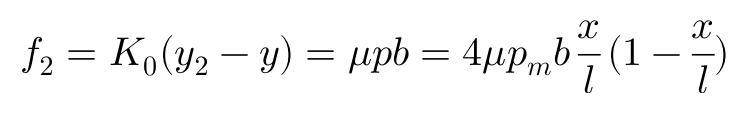
联合f1和f2的方程表达:
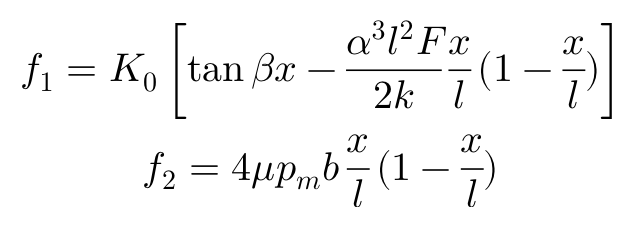
让f1=f2,求的L1的解为:
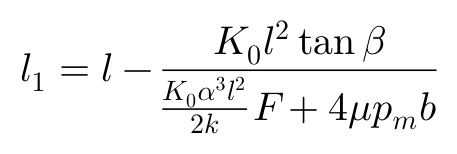
终于,我们知道了f1,f2,L1,现在终于可以针对接地区域的纵向各点做积分计算,求取侧向力的合力F了:
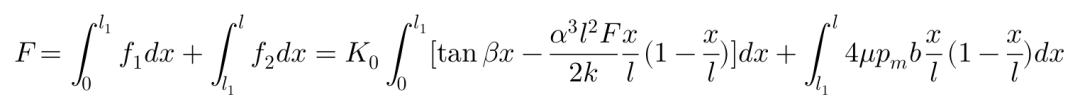
将L1方程带入方程F,Fiala对此近似求解得到:
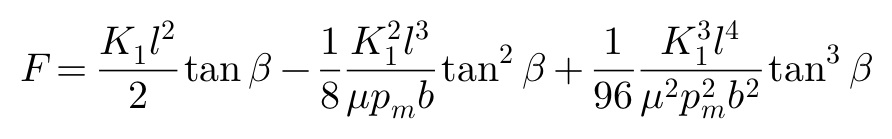
这就是轮胎侧偏角与侧向力的基本关系。其中:
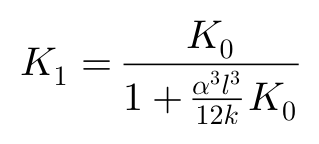
有了侧向力,我么再来看回正力矩。再回到轮胎变形模型的接地区图像:

显然,作用于轮胎接地面的侧向力并非对称于接地面的中心。于是,它将导致侧向力产生一个绕接地面中心的铅锤轴的力矩,也就是回正力矩。
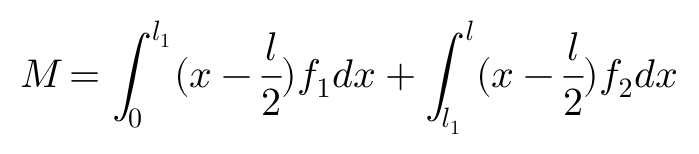
展开后:
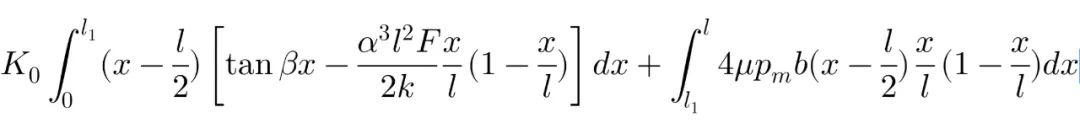
Fiala近似求解,得到轮胎侧偏角与回正力矩之间关系的基本方程:
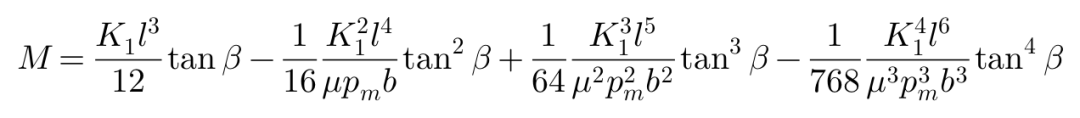
至此,我们得到了侧向力与侧偏角,回正力矩与侧偏角关系的数学方程。
问题是,这两个方程能带给我们什么有趣的信息呢?
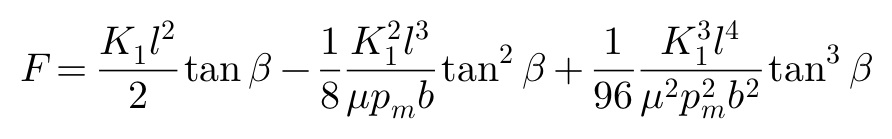
先看侧向力的方程,当β角很小的时候,单位侧偏角的侧向力(即侧偏刚度)可以表达为:
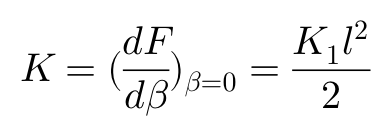
来看轮胎的最大摩擦力μW,已知:
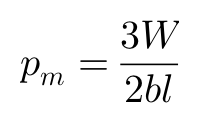
于是:
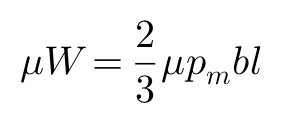
继续定义ψ为:
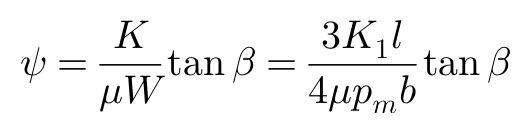
我们可以把关于F和M的方程转换为:
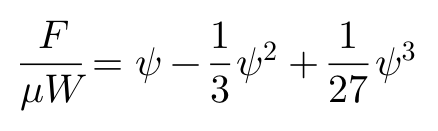
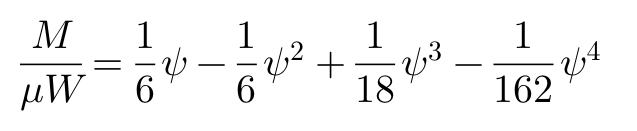
这便是1954年Fiala由简化的理论模型得到的无量纲解析式。
对以上两个方程进行微分计算,不难求得:
-
当ψ=3时,F/μW能够取得最大值。即F/μW=1
-
当ψ=3/4时,M/μW能够取得最大值。即M/μW=27/512
换言之,当侧向力F在侧偏角为:
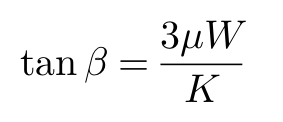
时为最大,其最大值为:Fmax = μW
同时,回正力矩M在侧偏角为:
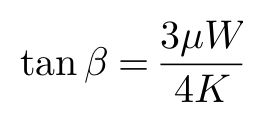
时为最大,且最大值为:Mmax = 27lμW/512
绘图表达的话,无量纲的侧向力F/(μW),回正力矩M/(lμW)和侧偏角ψ=Ktanβ/(μW)的关系为:
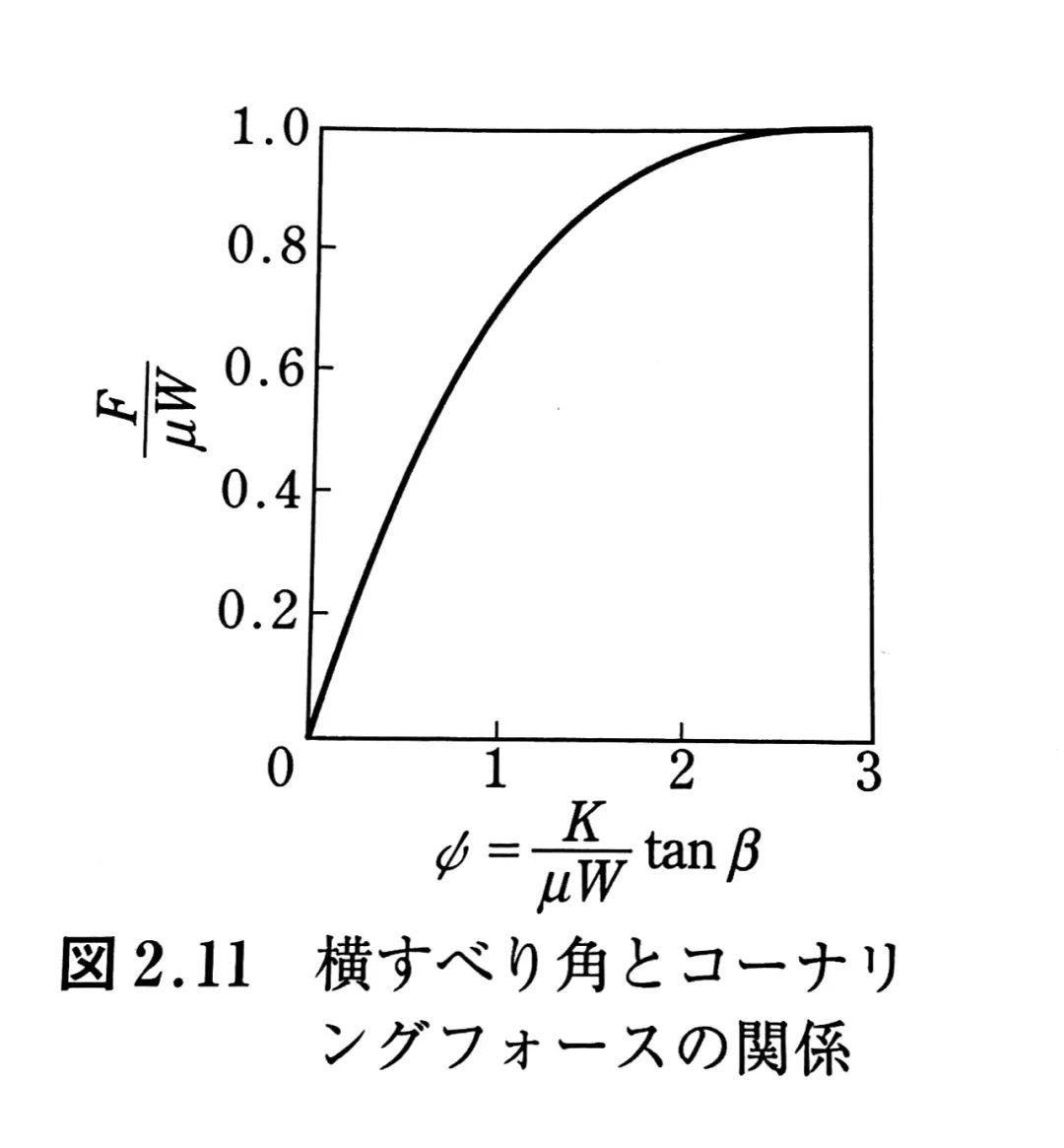
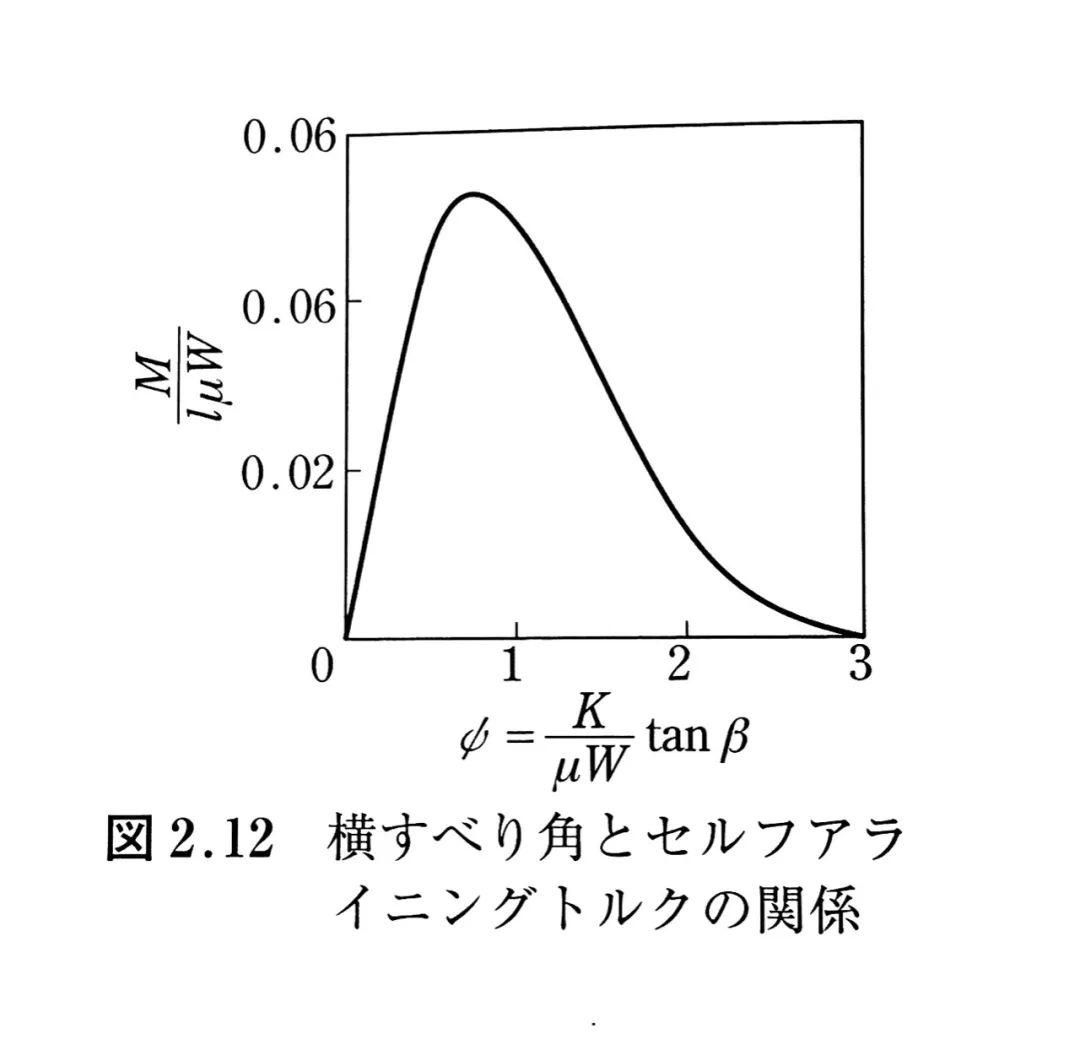
从图上观察,结论就比较清晰了:
-
当侧偏角β较小时,侧向力几乎与tanβ成正比。
-
当侧偏角β大于某个数值后,侧向力趋于饱和,不再随侧偏角增加而增大。
-
当侧偏角β较小时,回正力矩M几乎与tanβ成正比。
-
当侧偏角β大于某个数值后,回正力矩趋于饱和,并开始随侧偏角增加而减小。
总之,如果侧偏角β很小,则tanβ≈β,可认为侧向力和回正力矩均与β成正比。当侧偏角β很大时,侧向力不再与β成正比。
再进一步,当β的数值很小的时候,我们还可以省略掉二次及以上的项。
于是,对应于侧偏角β的侧向力和回正力矩可以被进一步简化为:
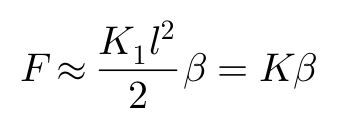
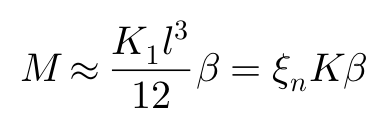
两个方程当中的K被叫做侧偏刚度,可以写成以下形式:
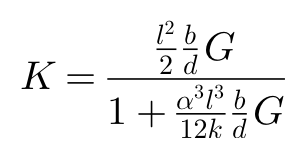
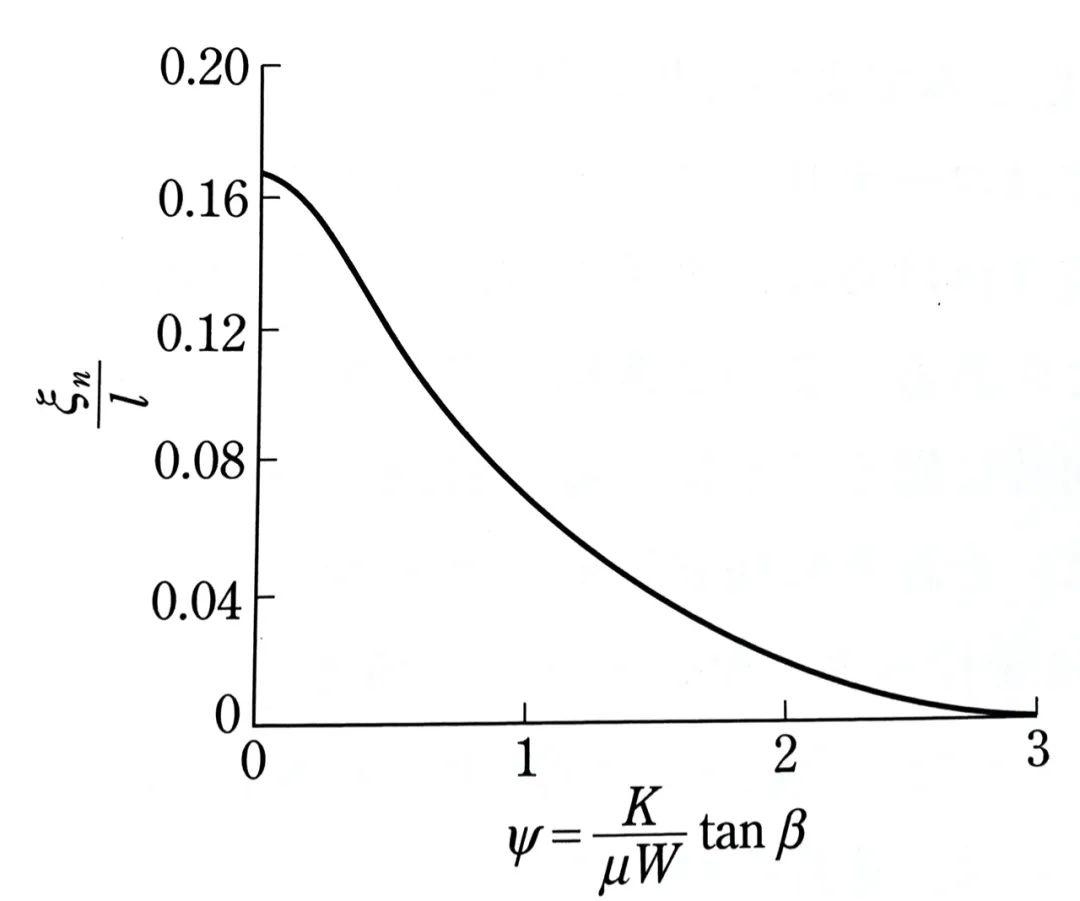
ξn代表的是轮胎拖距(pneumatic trial),即M/F的比值,用图形来表达,就是侧向力的作用点到接地区中心的距离。
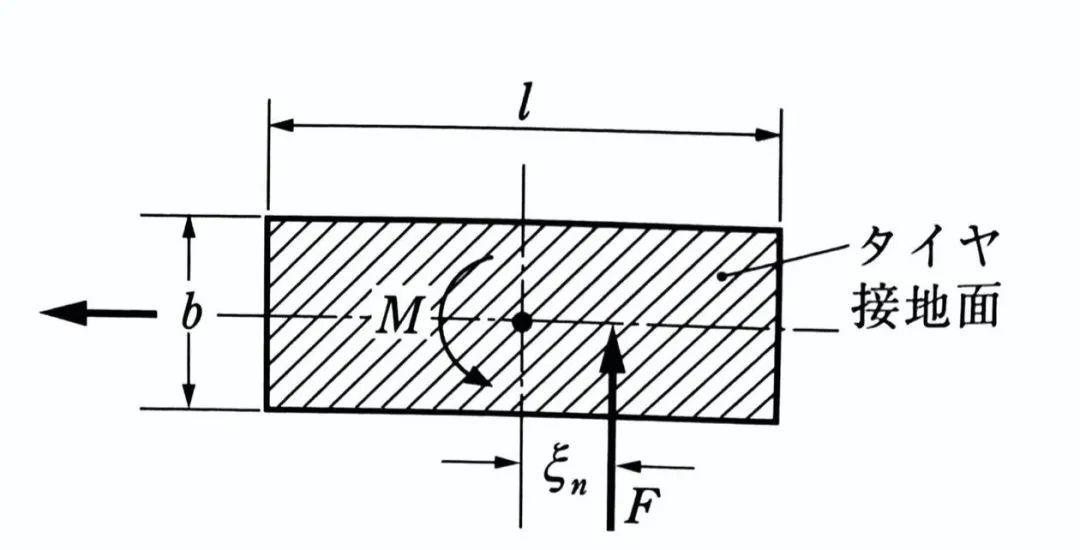
当β很小的时候,这个值是一个只跟l有关的值,从F和M的简化方程比值就可以求得:ξn=l/6。
好了,以上我们讨论了有侧偏角β时,作用在轮胎上的力。接下来,我们将考察有外倾角φ且保持直线行驶时轮胎所受到的力——外倾侧向力。
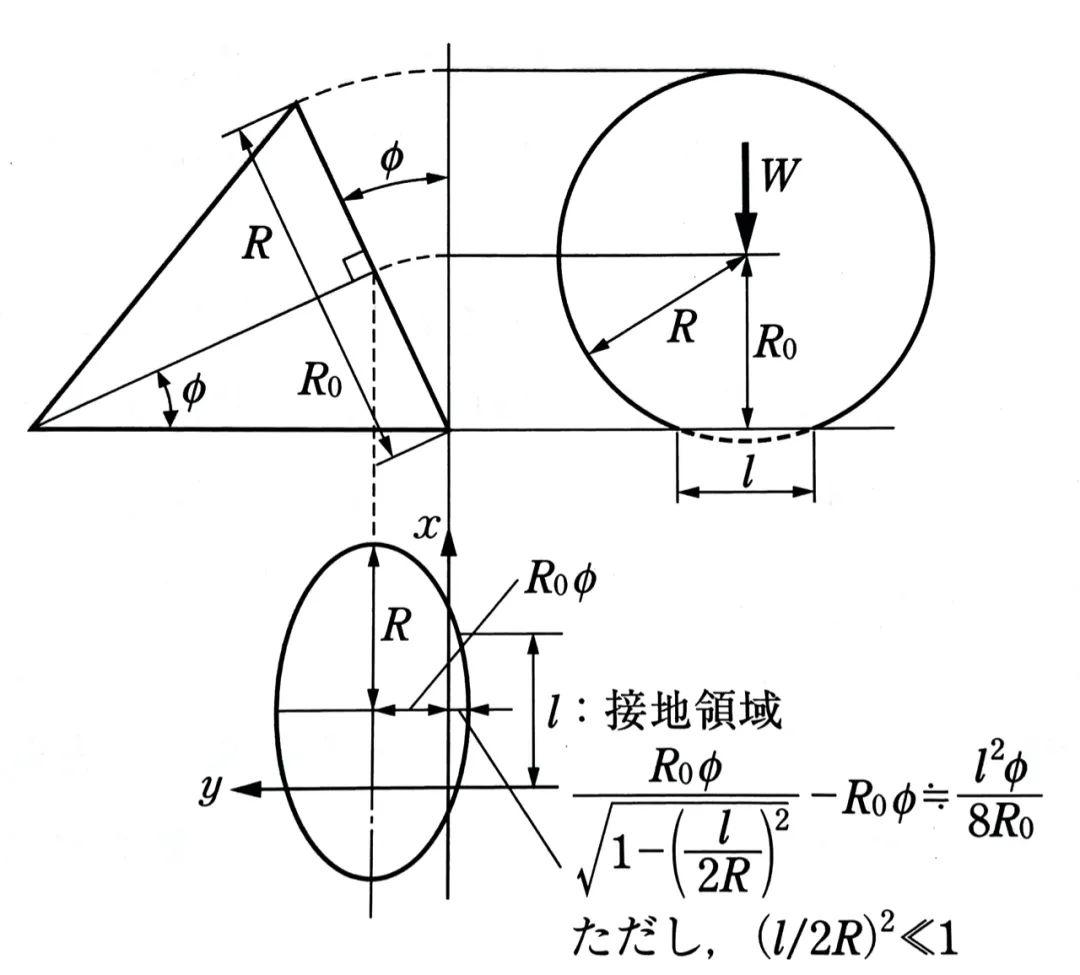
下面就是Fiala对有外倾角φ的情况作出的数学解析:
当考虑轮胎外倾时,即使不产生侧偏角,轮胎胎面基底的中心线也不是直线,而是一段圆弧。采用抛物线来拟合这个圆弧的话,就可以建立以下数学方程:
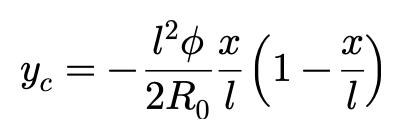
R0为轮胎胎面基底的有效半径,由下式给出:
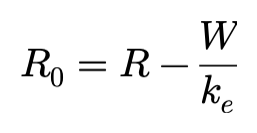
其中,R为无载荷时轮胎胎面基底的半径,ke为轮胎的纵向弹簧常数。
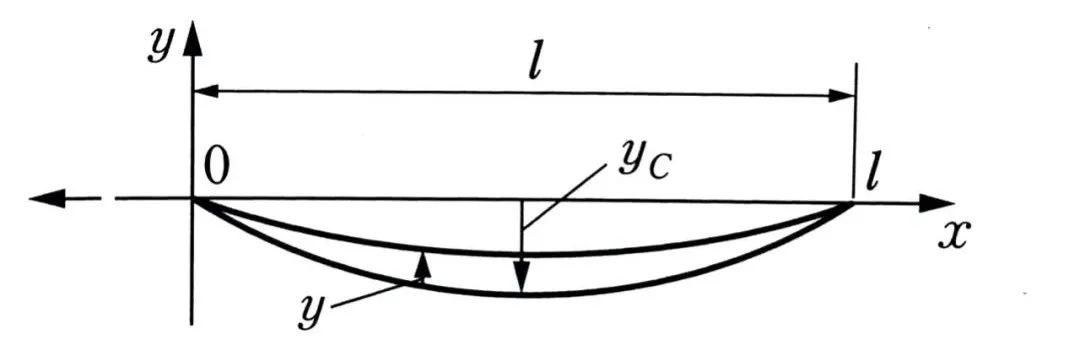
轮胎外倾时的胎面变形
如果轮胎在保持外倾角的状态下自由行驶,则轮胎胎面橡胶的接地区中心将会绘制出上图所示的弧形轨迹。如果轮胎只是做直线运动,则轮胎接地区中心应该沿着x轴运动——这就意味着,在轮胎胎面基底和地面之间的轮胎胎面橡胶上将产生剪切变形,这个变形带来的就是外倾侧向力Fe。
由Fe作用域接地区中心,产生的轮胎胎面基底变形可以表达为:
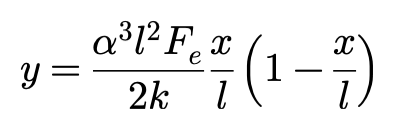
接地区距离x轴的位移为0,x方向各点上,轮胎胎面基底剪切变形为:-(yc-y)。作用于轮胎外侧的侧向力表达为:
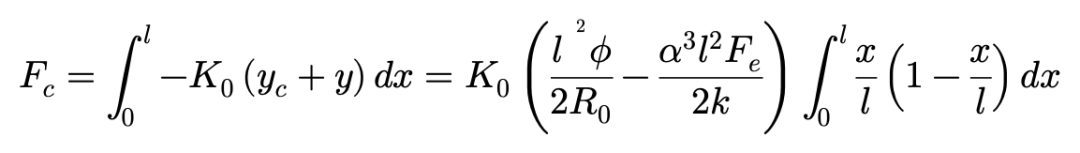
积分得到:
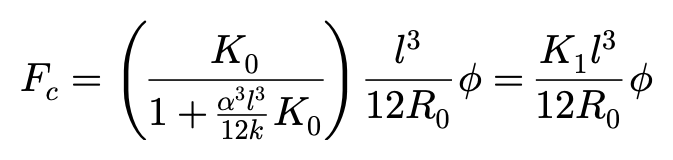
可以发现,外倾侧向力和外倾角成正比。比例系数为Kc:
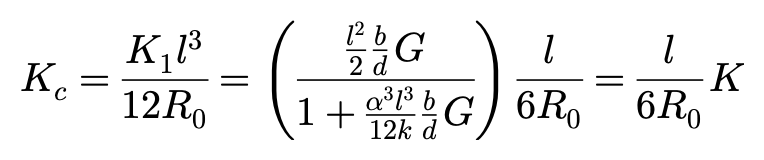
至此,我们建立了轮胎侧向力和力矩的一系列程,了解轮胎的侧偏特性,受到多个因素的影响:E,ν,I,b,d,k,l,μ,W:
E,ν:取决于轮胎胎面的材质和构造
I,b,d:由轮胎的形状决定
W:轮胎的垂直载荷
k:轮胎的充气压力决定,与气压成正比
l:取决于轮胎的形状,也受到轮胎垂直载荷雨充气压力的影响
μ:取决于轮胎的胎面材质和路面状态
综上,下面四个因素决定了轮胎的侧偏特性(关于侧偏力和回正特性):
-
轮胎的材质,构造和形状
-
轮胎的垂直载荷
-
轮胎的充气压力
-
路面状态
在实践当中,从这四个因素推倒出轮胎特性参数的影响很难实现。直接测量四个因素的影响也不容易。但是,测量具有侧偏角β、或者外倾角φ的轮胎侧向力F和力矩M则是可行的。
因此,接下来,我们可以做实验来直接得到结果来评估四种因素对于轮胎侧偏特性的改变和影响。
肆
普通轿车轮胎的侧向力与侧偏角之间的关系,不同的垂直载荷下的关系可以表达为:
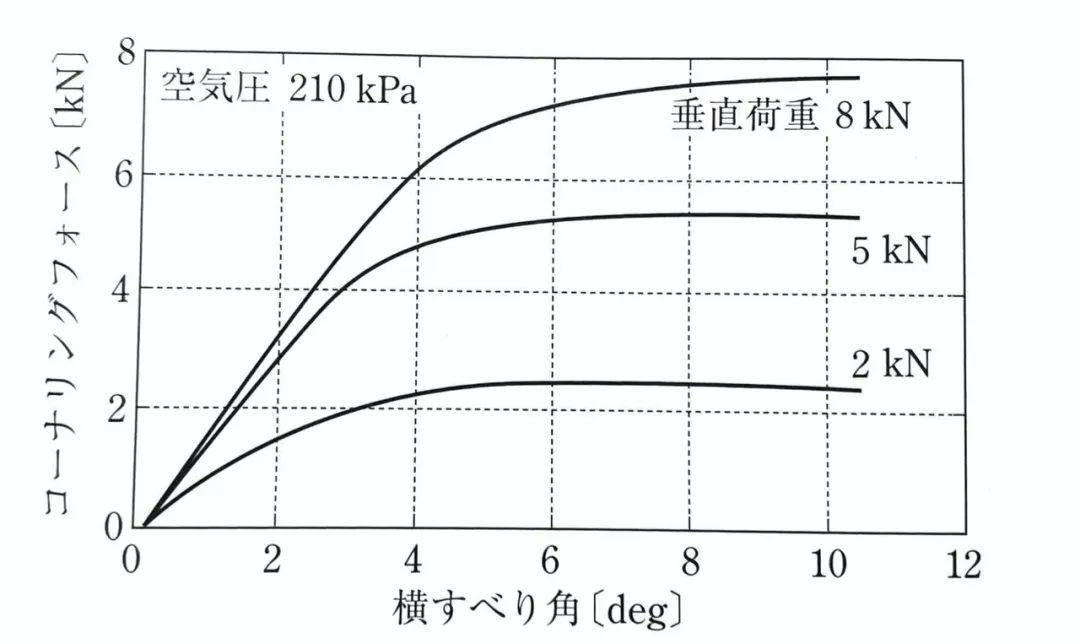
当侧偏角β小于4度左右时,侧向力是线性增加的。此后,侧向力的增加将放缓,并在8-10度时达到饱和。对于一辆普通轿车而言,侧向运动通常是在线性区域范围内发生的。
图上曲线的斜率,就对应着轮胎的侧偏刚度——即单位侧偏角产生的轮胎侧向力,是评价轮胎侧偏特性的一个重要参数。
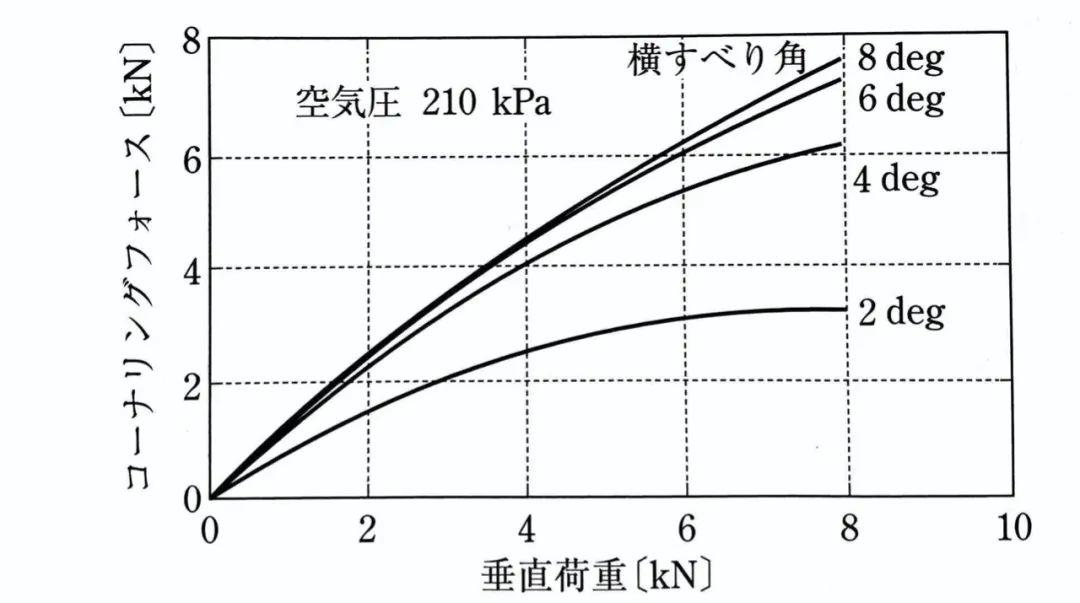
继续,上图展示了垂直载荷对侧向力的影响。
侧偏角很小时,轮胎的垂直载荷对侧偏力几乎没有影响。随着侧偏角的增加,侧向力的饱和值之间的差异变得显著。
这一规律可以从模型推理直接获得:实际上,如前文所述,只有在轮胎胎面基底与地面发生相对滑动的区域,轮胎的垂直载荷才能对侧向力产生影响。当相对滑动的区域越多时,即侧偏角很大的情况下,轮胎侧向力的大小将接近摩擦系数和垂直载荷的乘积——此时垂直载荷的影响最为显著。
继续深入,我们再研究下轮胎垂直载荷对轮胎侧偏刚度的影响。
从侧向力和侧偏角的关系可以推导出,当轮胎载荷较小时,侧偏刚度会随着载荷的增加而增加,但当载荷超出某一极限的时候,侧偏刚度可能会减少。
我们引入一个新的概念:侧偏刚度系数。
侧偏刚度系数是侧偏刚度与此时载荷相除得到的数值。
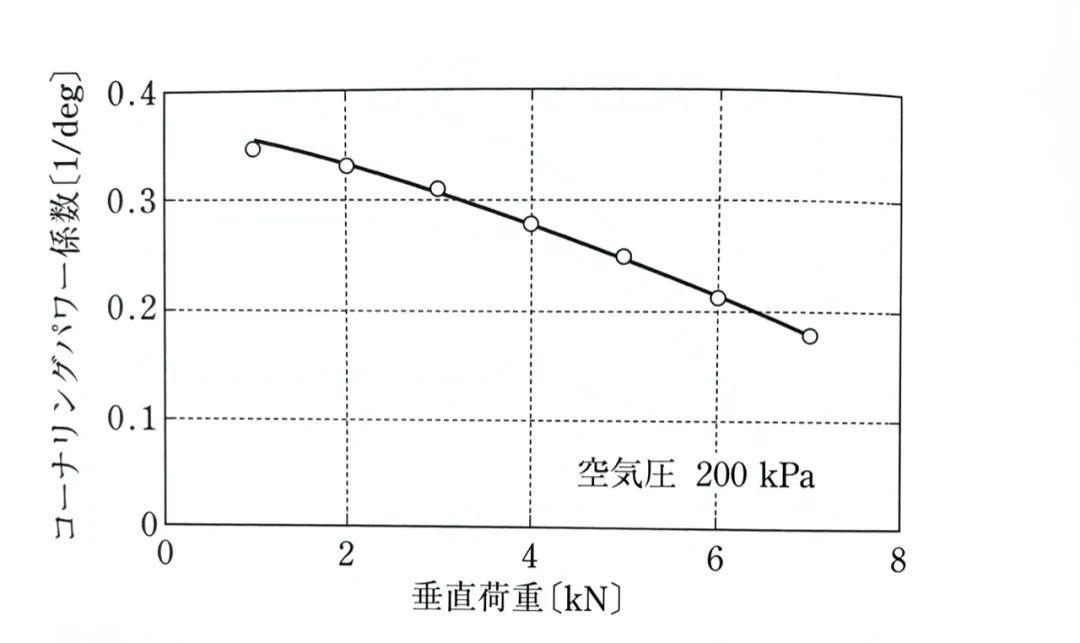
图中展示了载荷与侧偏刚度系数(即侧偏刚度/载荷)之间的关系
侧偏刚度系数随着轮胎载荷的增加而线性减少——对这一规律建模,侧偏刚度和轮胎载荷的关系可以写为:
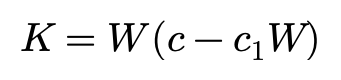
c为载荷在零附近的侧偏刚度系数,c1为其载荷相关系数。
这个方程告诉我们,轮胎的侧偏刚度与轮胎的载荷曲线可以近似为一条经过原点的抛物线:侧偏刚度随轮胎载荷的增加而达到一个峰值,之后随着轮胎载荷的增大而减小。
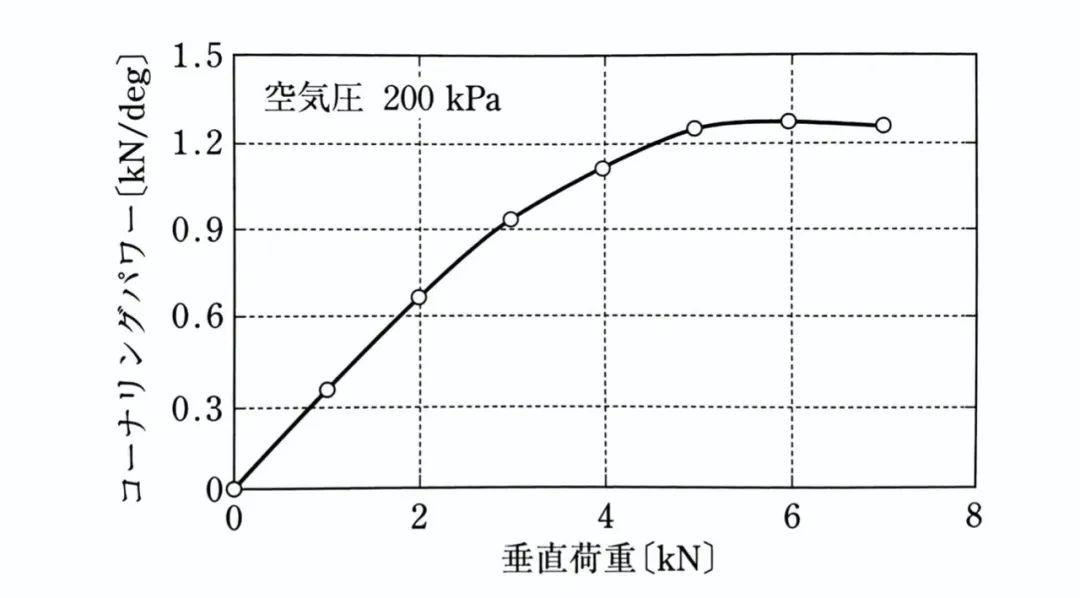
而轮胎通常在侧偏刚度随载荷增加的范围内工作。
摩擦系数对侧向力的影响
如果我们把垂直载荷的影响用μW来表达的话,可以定性的分析伴随轮胎侧偏角的变化,不同路面摩擦条件对侧向力的影响:
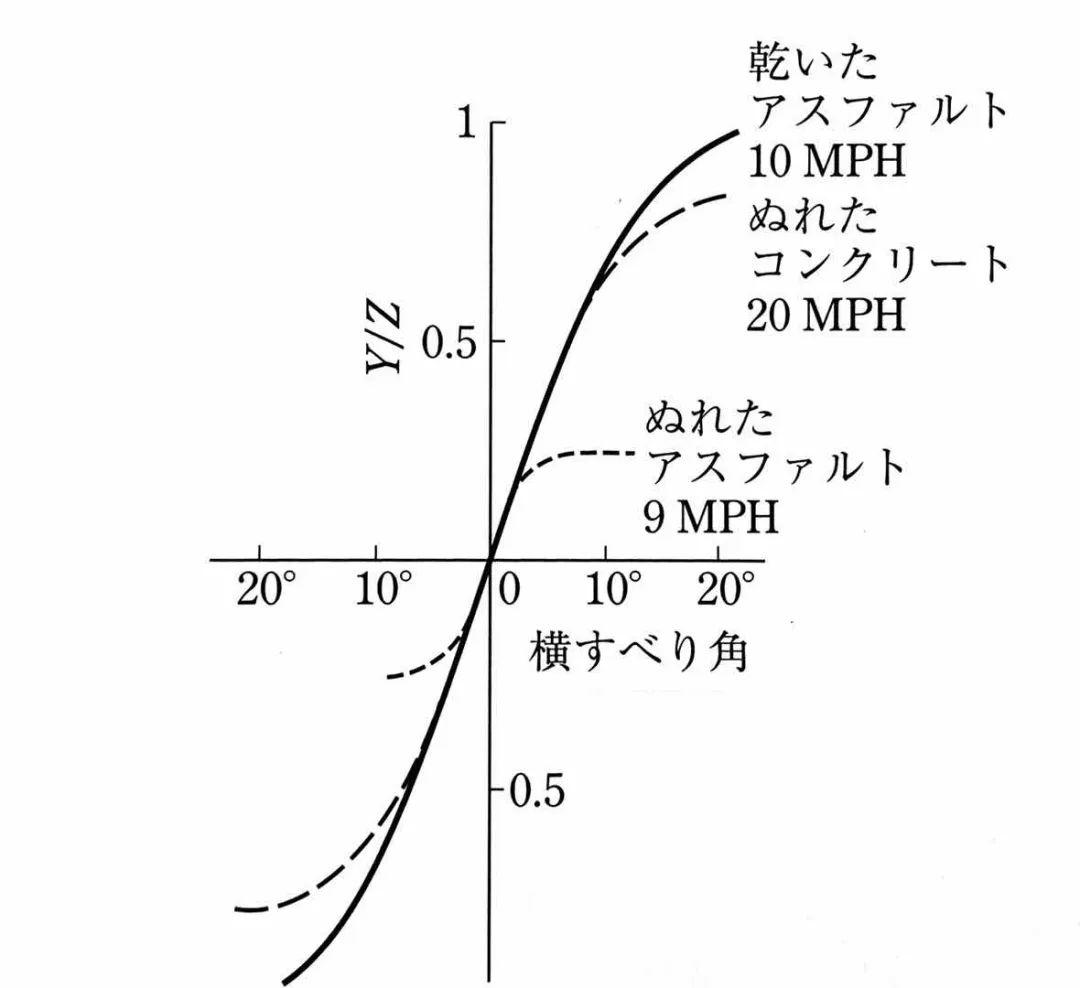
干沥青10mph,湿混凝土20mph,湿沥青9mph,不同路面条件对侧向力的影响
从上图可以看到,当侧偏角较小时,摩擦系数对侧向力几乎没有影响,而当侧偏角较大时则有显著影响。这就意味着:摩擦系数对侧向力的影响与垂直载荷的影响是相似的。
胎压对侧向力的影响
对某一恒定的力而言,轮胎胎面基底的变形y越小,轮胎的侧向力就越大。而想要轮胎胎面基地变形y更小的话,轮胎弹性基础的弹簧常数k,以及轮胎胎面基底的弯曲刚度EI就要越大。
由于弹簧常数k取决于轮胎的充气压力,因此可以预测:侧偏力应该会随着轮胎充气压力的增大而增大。
但是增大轮胎充气压力会降低接地的长度l——这会使得侧向力随着接地区长度减少而减少。
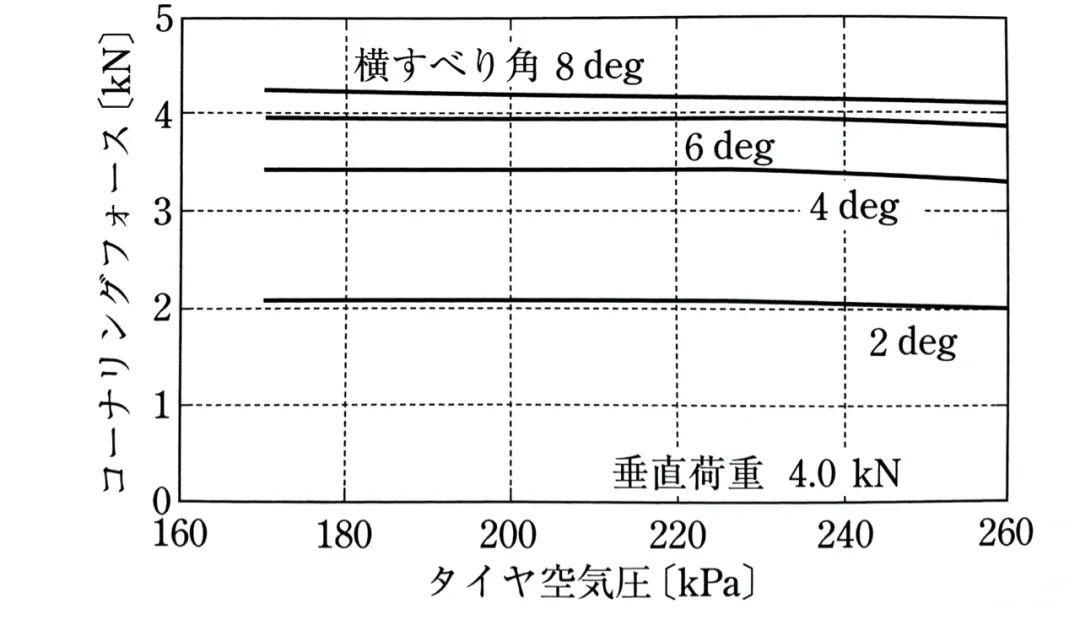
两相作用的结果就是一个有趣的现象:一定充气压力变动范围内,侧向力几乎不受充气压力的影响。
这个现象还可以通过另一个实验佐证,即侧偏刚度和充气压力之间的关系:
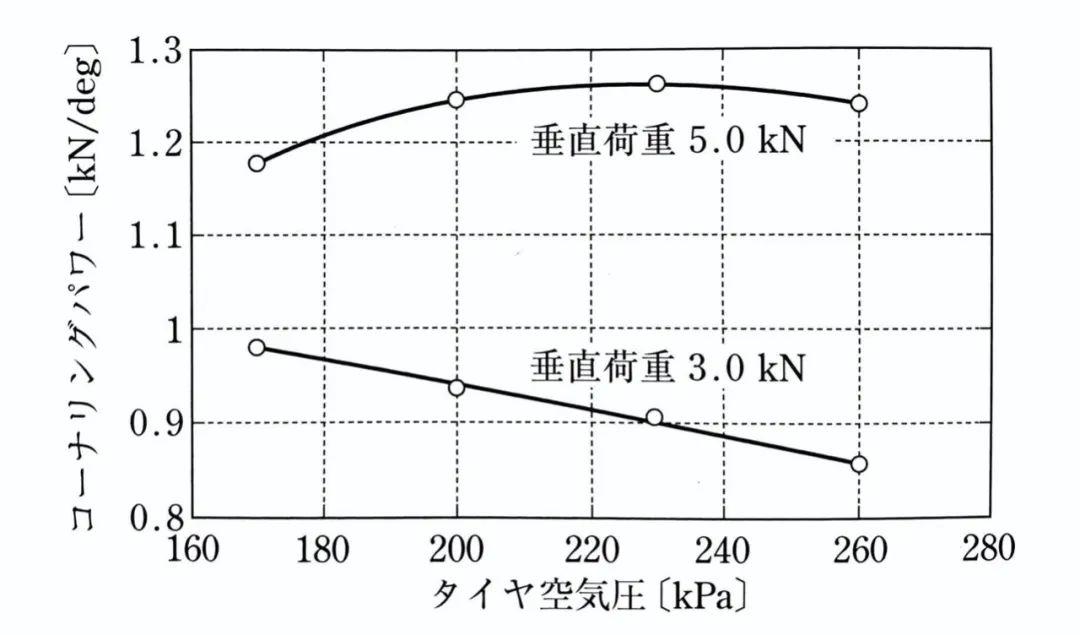
-
当垂直载荷相对较小时,接地区长度对侧向力的影响比弹簧常数k大,即此时的侧偏刚度随着轮胎充气压力的增加而减小。
-
当垂直载荷相对较大时,弹簧常数k对侧向力的影响比接地区长度大,即此时的侧偏刚度随着轮胎充气压力的增大而增大。
轮胎形状对侧向力的影响
轮胎胎面基底的弯曲刚度EI由轮胎的形状决定。如果给定轮胎的材质和构造,则轮胎形状受到的影响主要取决于轮胎胎面基底的转动惯量I。
也就是说,轮胎的尺寸越大,转动惯量I值越大。
对于半径相同的轮胎,宽度越大,越扁平,转动惯量I值越大。
于是,为了获得更高的侧向力,我们会倾向于把轮胎制造成扁平的形状。这也是我们在运动型车甚至跑车上能够看到的现象。
当宽度b增大,厚度d减小时,轮胎的侧偏刚度会增大。这可以从实验数据当中,轮胎胎面橡胶厚度相当的轮胎胎面沟槽深度和侧偏刚度的图形关系中发现端倪:
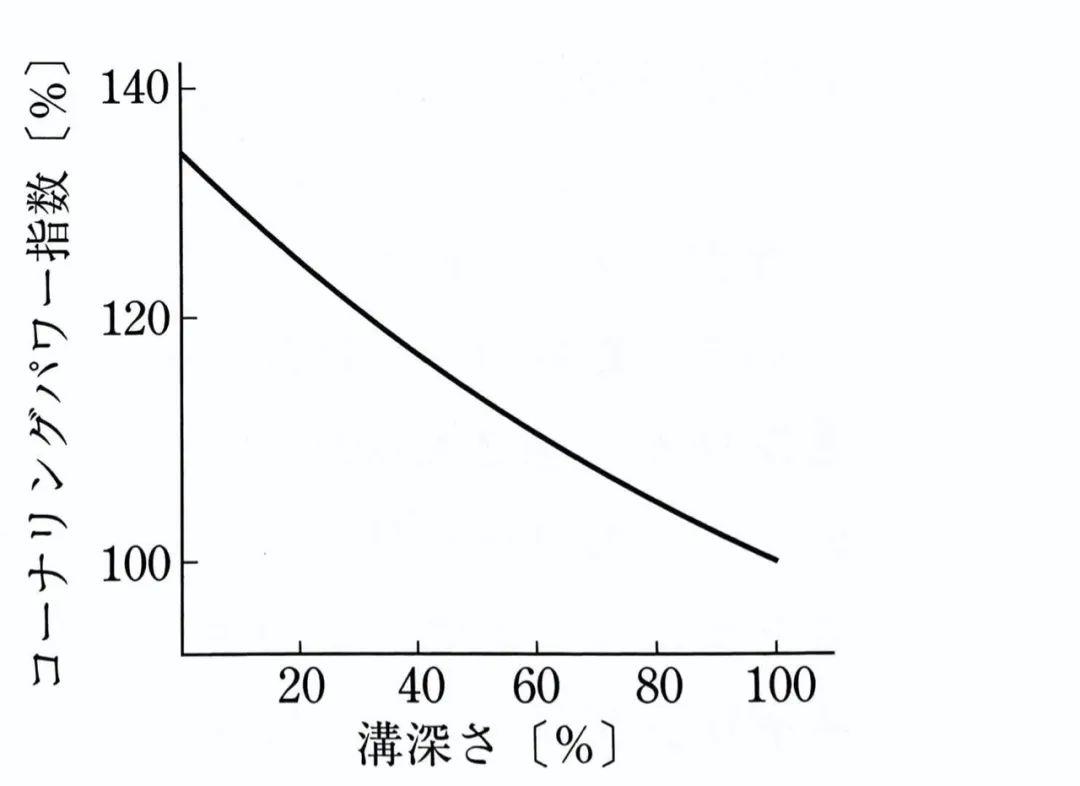
从图形中可以发现,当轮胎胎面磨损使得轮胎厚度d减小时(等效沟槽深度变小),侧偏刚度将会增加。
驱动力和制动力对侧向力的影响
在制动或驱动过程中,轮胎不仅会受到支撑车辆荷重的垂直载荷,还受到车辆制动或驱动的纵向力——这会影响轮胎的侧向力。
为什么?
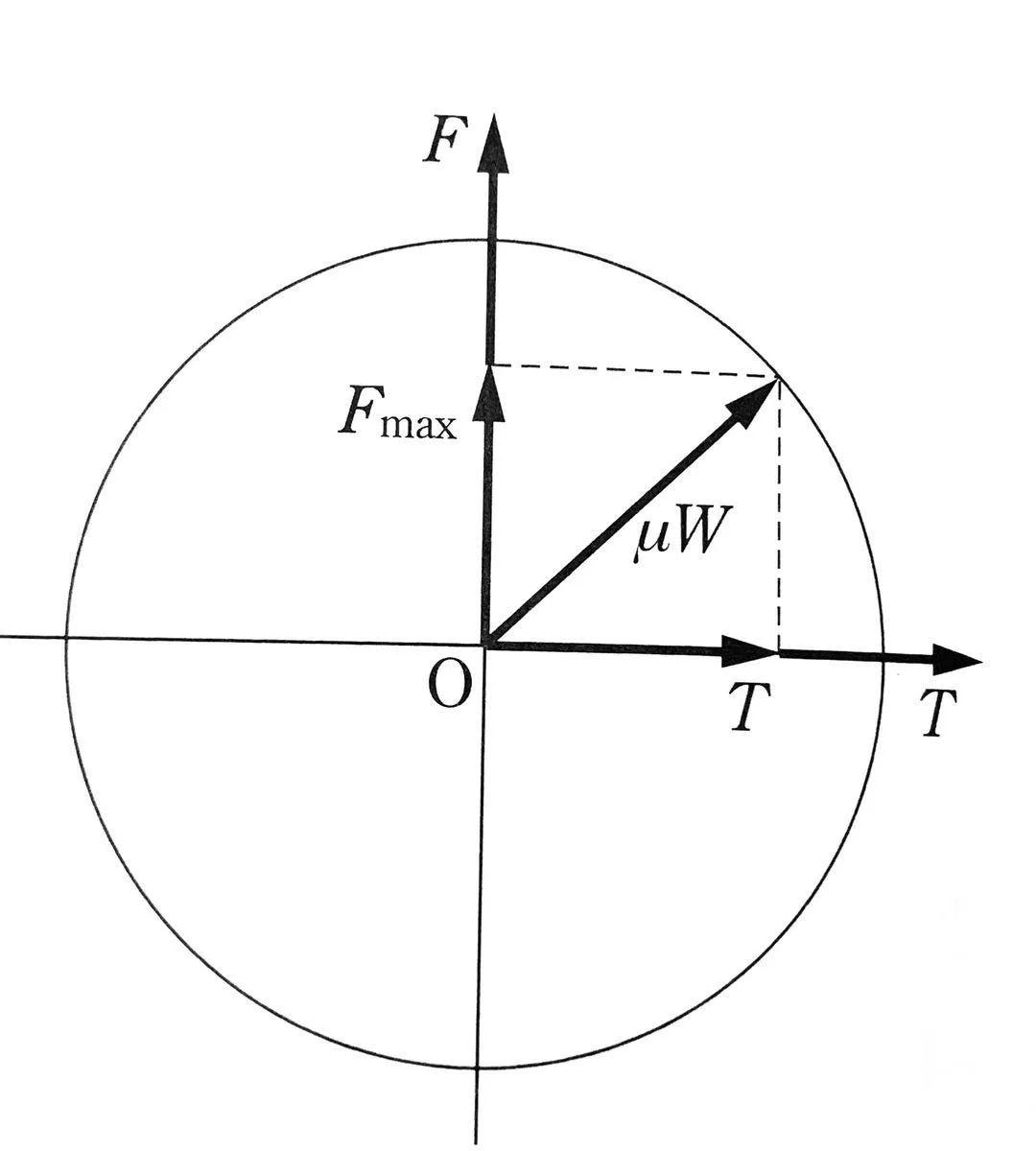
这就是经典的“摩擦圆”理论了。摩擦圆是说,作用域轮胎上的侧向力F和驱动力(或制动力)T总是满足以下不等式:
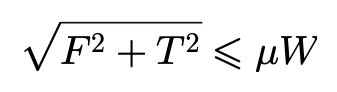
也就是说,作用在轮胎与地面接触面内的水平合力不会超过其垂直载荷与摩擦系数的乘积。合力的矢量只能位于半径为μW的圆——摩擦圆内。
如果轮胎在纵向收到的驱动力或者制动力的作用,则在大偏角时能达到的最大侧向力,可以表达为:
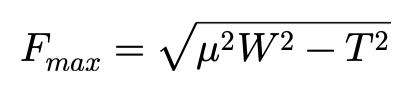
如果T=0,则上式将变为我们熟悉的一般形式:Fmax = μW
如果摩擦圆加入侧偏角的图形化表达,我们就会得到这样的图样:
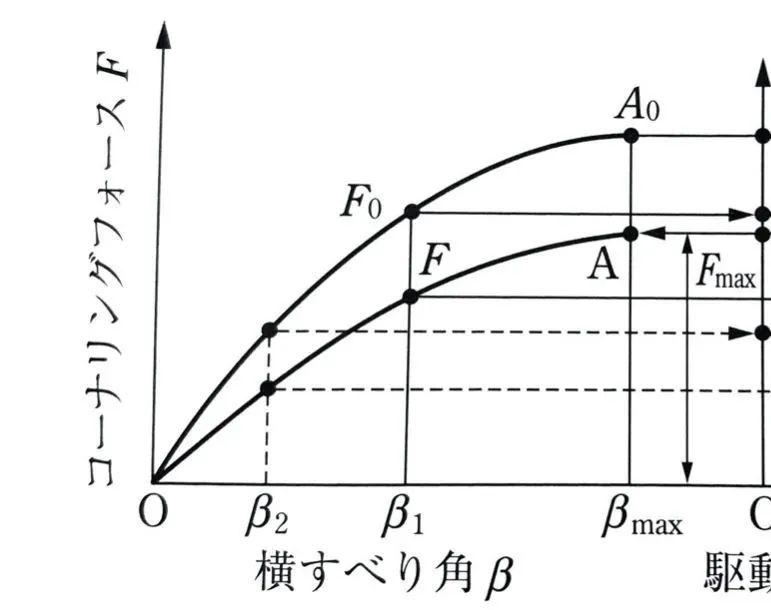
当驱动力或制动力为零时,侧向力F0与侧偏角β的关系,可以用图上的曲线段OA0表达。当考虑到驱动力或者制动力(不为零)时,侧向力将不会到达A0的高位,曲线段OA代表了这一情形。
我们假设:不论侧偏角时多少,在任何值时,由驱动力(或制动力)引起的侧向力的下降率是相同的,则将建立以下方程:
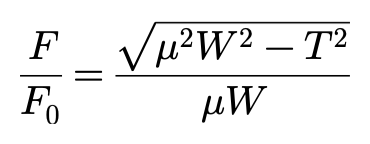
或者可以写成椭圆曲线方程:
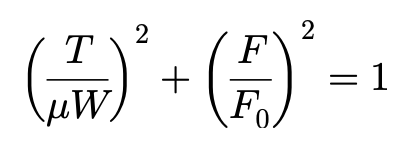
按照方程的定义,对于给定的侧偏角,侧向力F与驱动力或制动力T的关系曲线是椭圆:
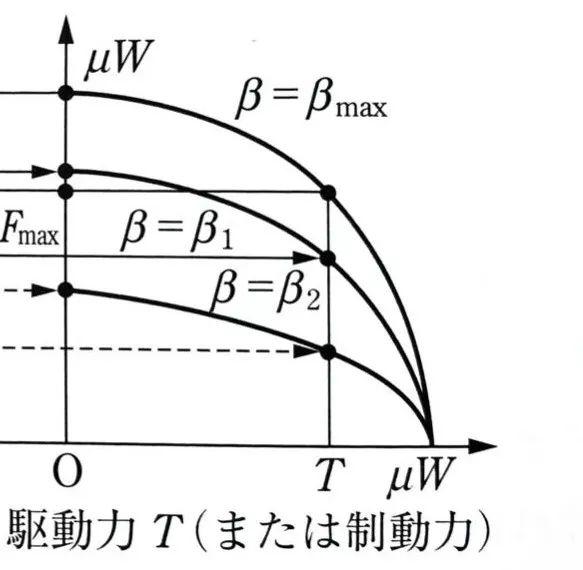
关于驱动力和制动力对侧向力的影响,人们实践当中做了很多研究。从实测值当中,我们也能得到关于摩擦圆的图像直觉:
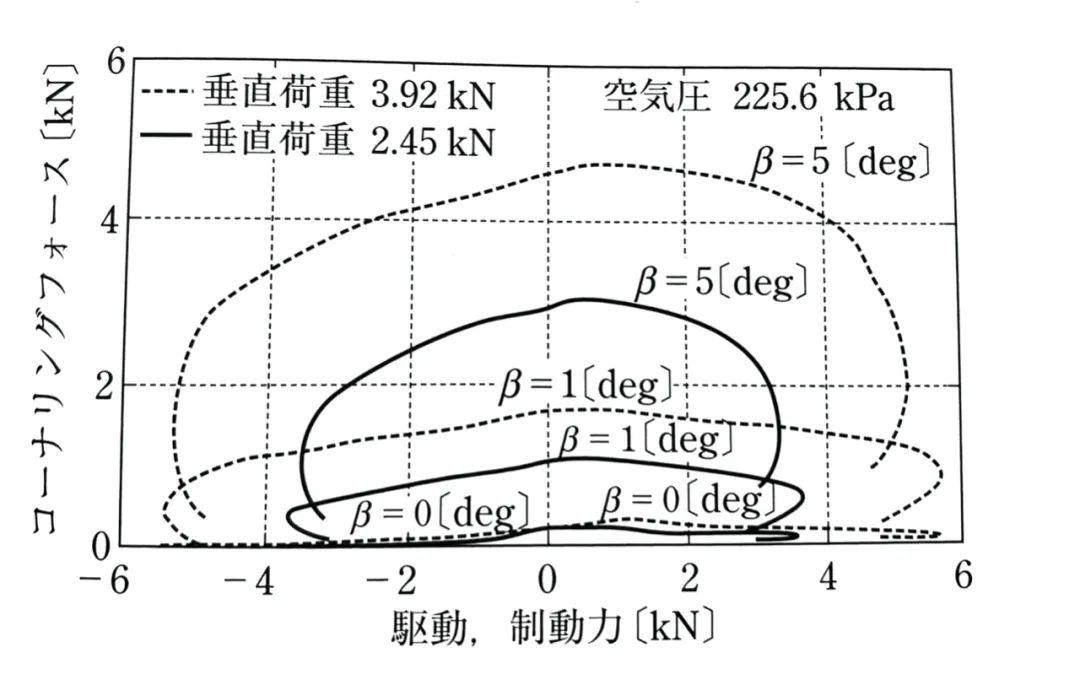
有驱动力(正向)和制动力(负向)作用下的侧向力(纵轴)
侧偏角对回正力矩的影响
来看一个真实的测试数据,展现侧偏角与回正力矩之间的关系:
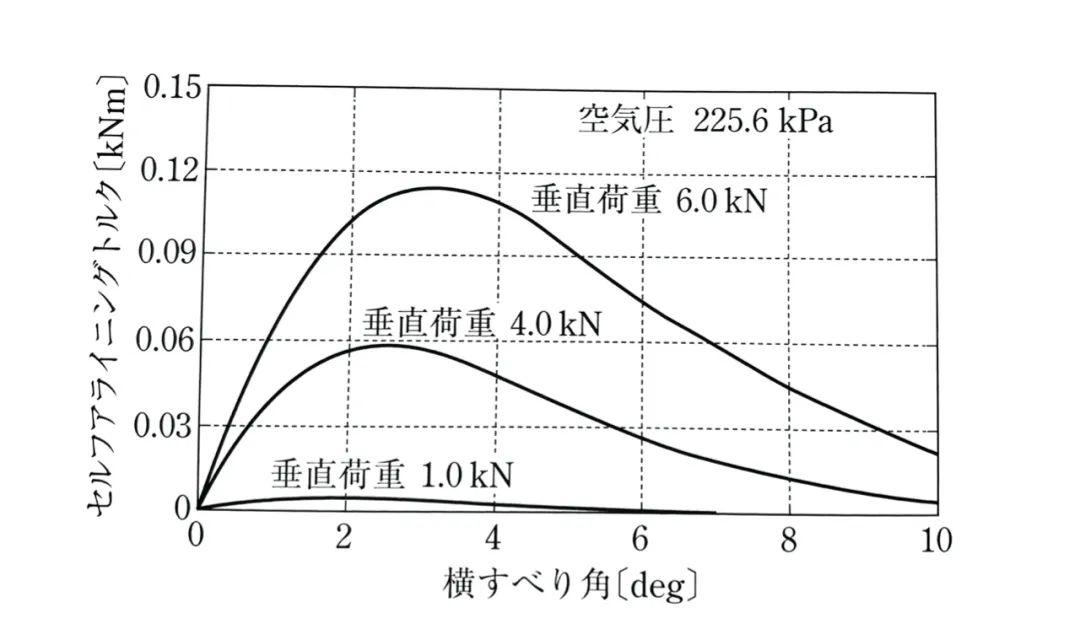
关于侧向力,我们知道:
-
侧偏角较小时,轮胎垂直载荷对侧向力的影响较小。
-
侧偏角较大时,轮胎垂直载荷对侧向力的影响显著。
而这张图告诉我们,无论侧偏角如何,轮胎垂直载荷对回正力矩的影响都很大。
一个原因是:垂直载荷的影响发生在轮胎接地区与轮胎橡胶之间存在相对滑动的范围内(即部分接地区),而回正力矩是前后两个接地区侧向力影响下作用的结果。因此载荷越大,其对回正力矩的影响就越大。
另一个原因是,轮胎垂直载荷的增大会导致接地区长度增加,因此侧向力产生的力矩也会增加,如果你还记得回正力矩M的数学表达式,你就会发现方程当中包含了l的三次方项以及更高的项。
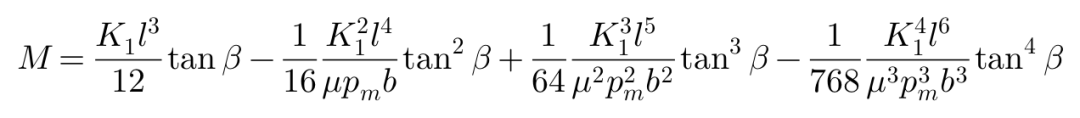
胎压对回正力矩的影响
对于一个真实的轮胎来说,回正力矩可能会随胎压增加而降低。
原因是:如前文所述,虽然侧向力随着轮胎充气压力增加而增加,但与此同时接地区的长度减小了——这会对会整理句产生不利影响。
反过来,降低充气压力,回正力矩会增加,但是当压力低于某个值时,回正力矩将不再增加了——因为这时,侧向力的减小对回正力矩的影响比气压降低更加显著。。
一旦侧偏角增大,轮胎拖距ξn(如果你还记得,这代表了回正力矩和侧向力的比值)就会急剧减少,因此。
外倾角对外倾侧向力的影响
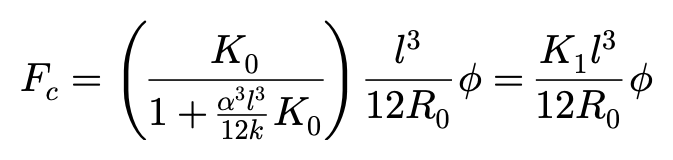
从外倾侧向力的公式可知,当侧偏角为零时,轮胎的外倾侧向力和外倾角成正比。
实验也得出了同样的发现:
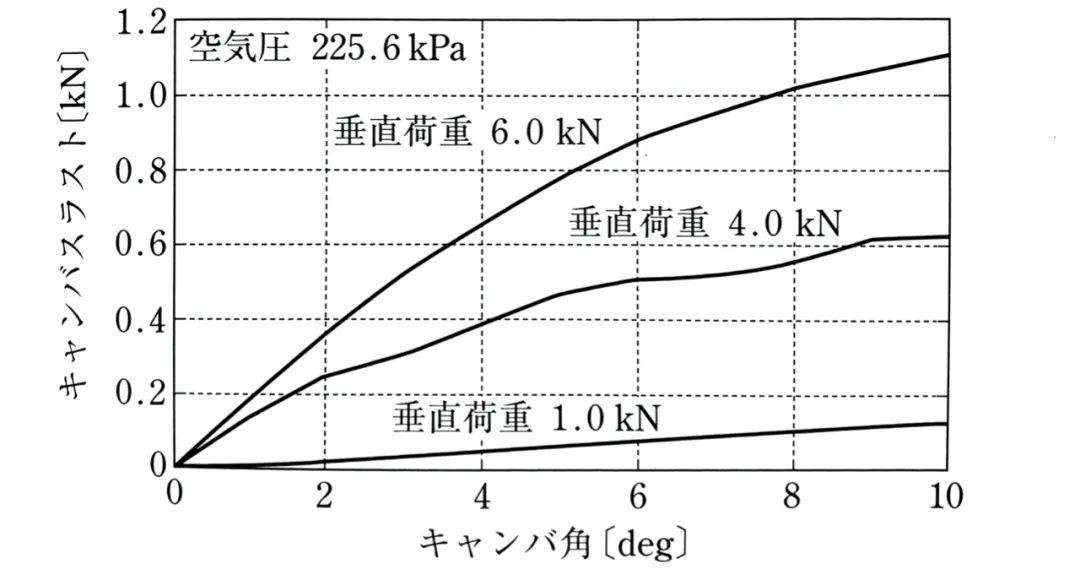
从图上还可以发现,单位外倾角对应的外倾侧向力(外倾侧向力系数,即曲线的斜率)几乎随着轮胎垂直载荷的增加而线性增加。
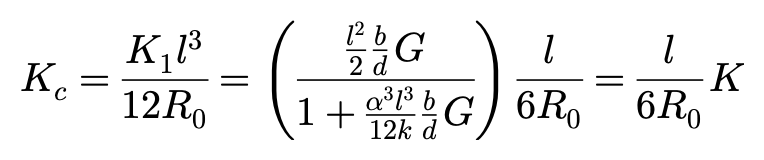
实际上,外倾侧向力系数取决于垂直载荷,并随着垂直载荷的增大而增大。从该方程还能发现,外倾侧向力系数等于侧偏刚度和l/6R0的乘积。
由此可以断定,外倾侧向力系数与侧偏刚度有着相似的特性。
轮胎接地缺长度l和有效半径R0的比值l/R0通常在0.3左右,因此外倾侧向力系数通常小于侧偏刚度的1/10:
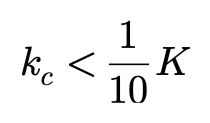
侧偏角和外倾角对侧向力的影响
车辆行驶过程中,往往同时存在侧偏角和外倾角,Ellis就研究了侧偏角和外倾角共同作用产生侧向力的情况。
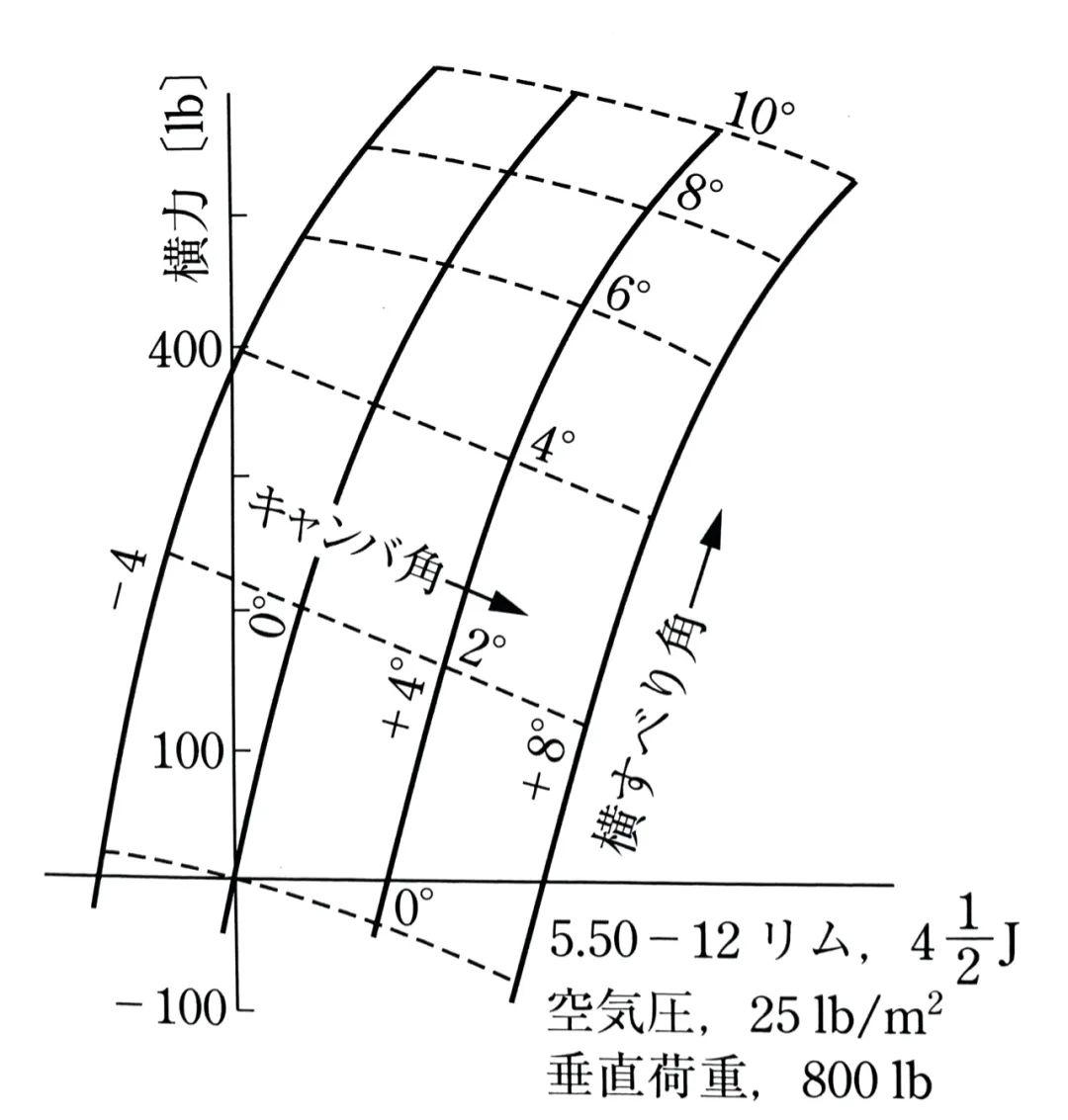
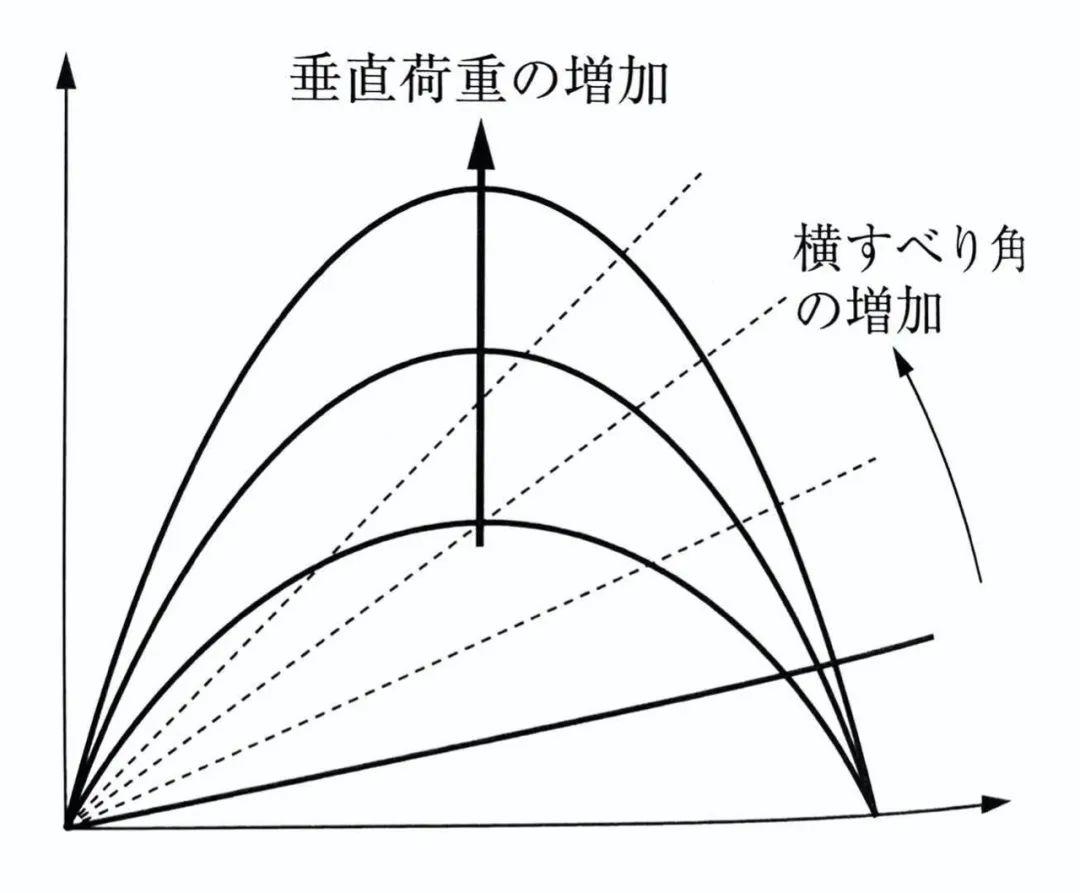
Ellis的研究给出了一个有趣的结论:不同外倾角下(即图上的キャンバ角),侧偏角(即图上的横すばり角)与侧向力的关系曲线近乎平行——这就意味着,外倾角和侧偏角产生的作用于轮胎上的侧向力可以独立地进行处理。
在轿车上,通常使用的扁平轮胎导致与以上规律产生出入,原因在于,当发生外倾时,扁平轮胎的接地区内,轮胎载荷的侧向分布很容易形成内侧轮胎载荷大,外侧载荷小的情况。

轮胎载荷减少会引起侧向力的下降,轮胎载荷增加会引起侧向力增加。
通过侧偏刚度和载荷关系图对两者进行对比的话,前者的影响更加显著,因此扁平轮胎总体所产生的侧向力会小于载荷均匀分布的情况。
在侧偏角和外倾角共同影响下,总侧向力更加接近以下卡丁车扁平轮胎的研究结果:
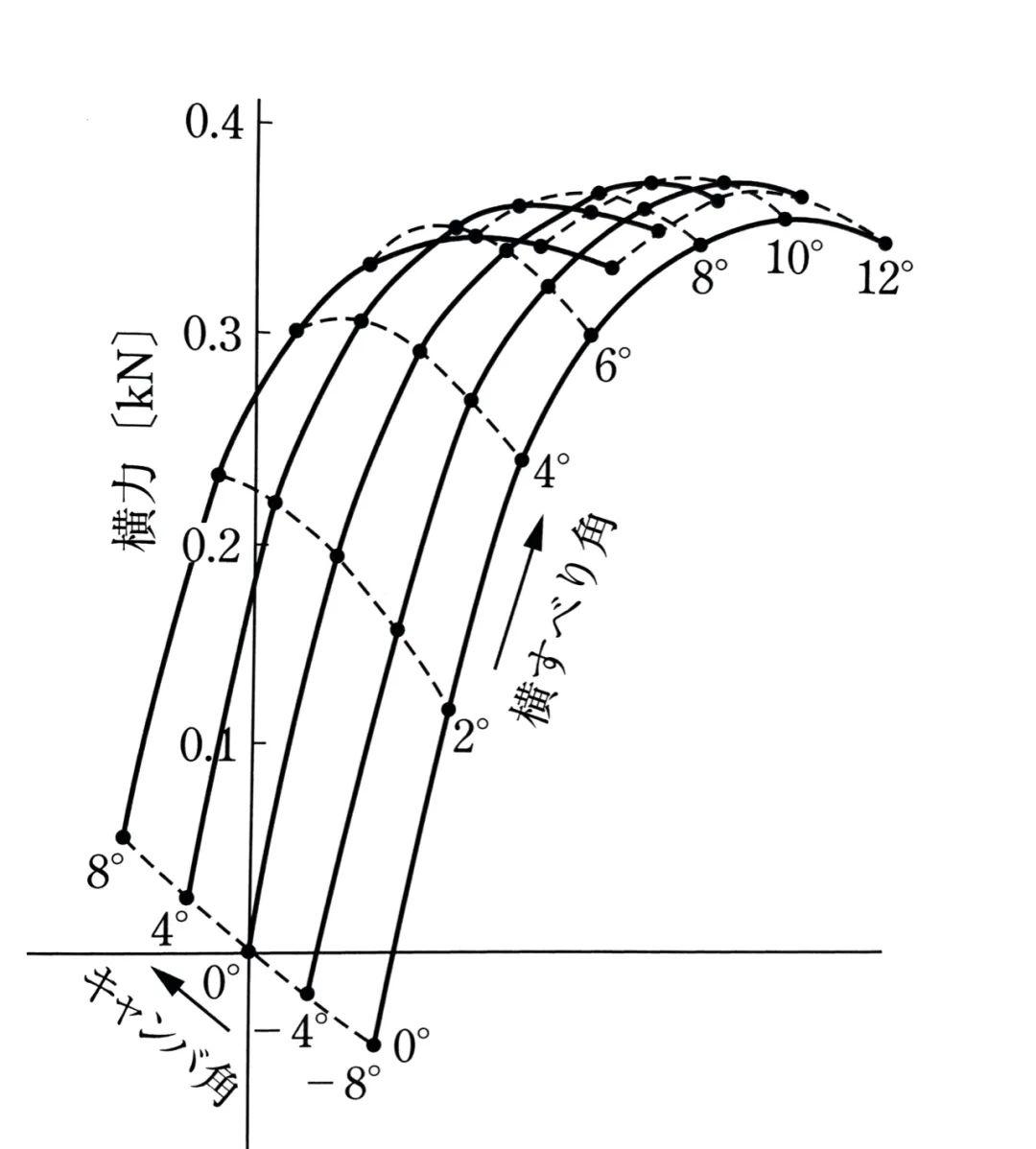
与Ellis研究的不同之处在于:虽然主要是侧偏角决定了侧向力,两者为同一方向,而外倾角决定的外倾侧向力比重较小。但由于外倾角还会引起轮胎载荷分布的变化,这个变化会导致侧向力的减小,因此由侧偏角和外倾角引起的总的侧向力会减少。
伍
上一节中提到了驱动和制动情况下,利用摩擦圆来定性地分析轮胎的侧偏特性。但这个模型却过于粗放,更合适的方式是如第二节一样,利用Fiala理论建模来研究驱动和制动工况下轮胎的侧偏特性——即伴随轮胎滑动,胎面基底相对轮辋发生弹性变形,同时胎面橡胶相对胎面基底进一步发生变形。
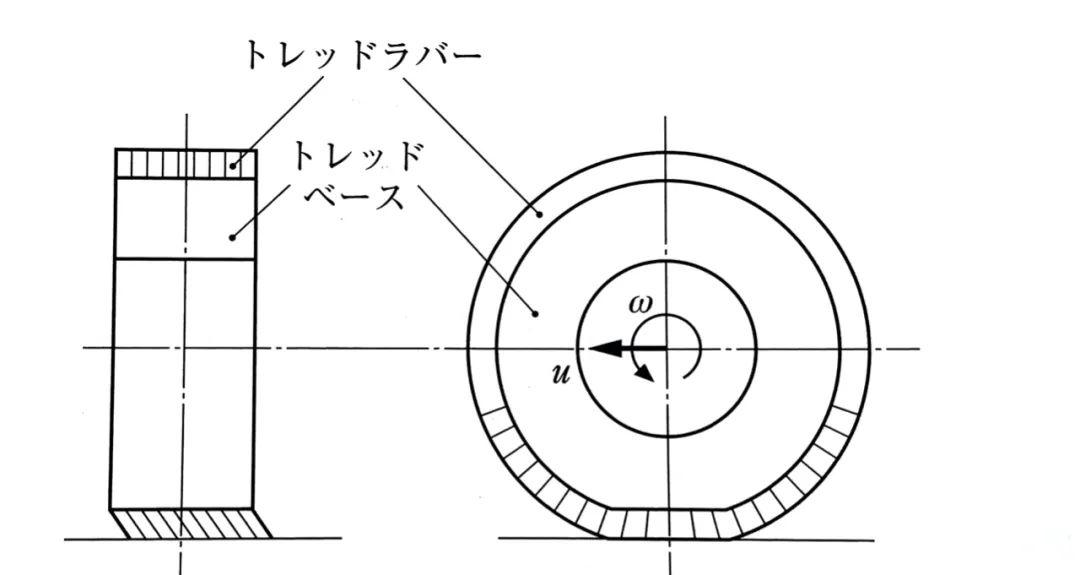
但这样思考会让模型变得过于复杂。取而代之的是,我们将轮胎胎面基底作为唯一的弹性部分。这样一来,我们就能够同时考察纵向和横向的弹性变形了。
这就是“刷子模型”,再刷子模型里,轮胎胎面橡胶并非环状的连续体,而是由沿轮胎周向的无数个独立的弹性体构成。
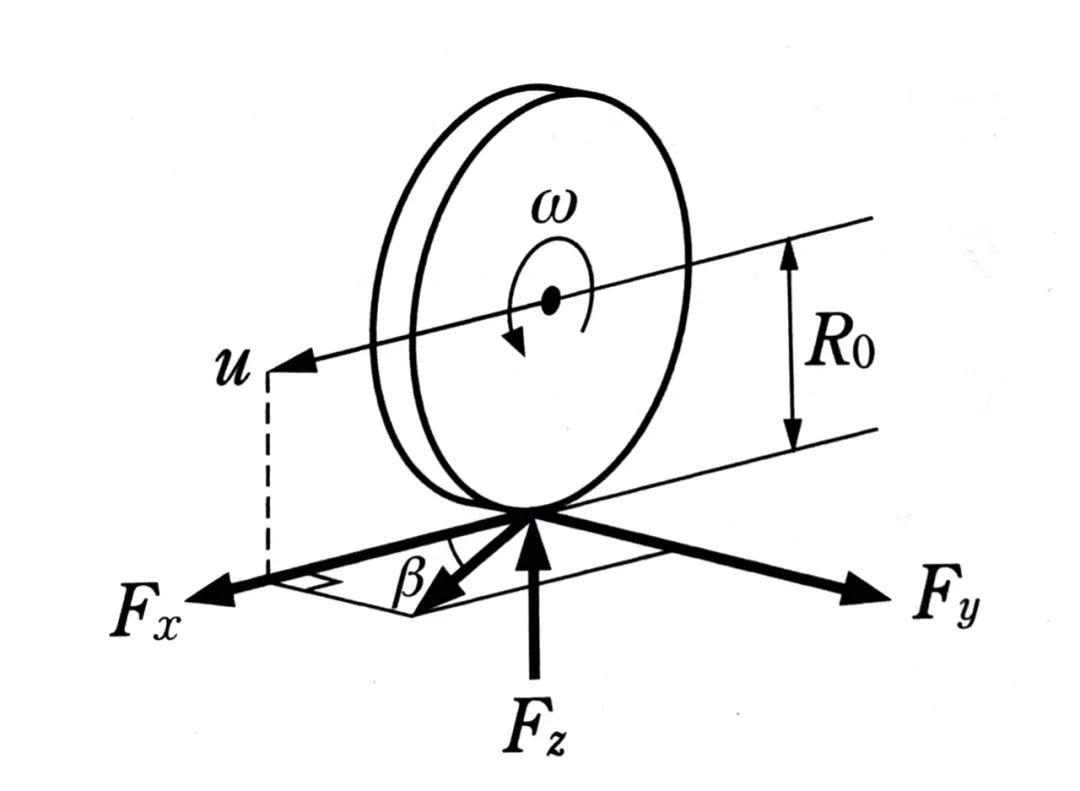
制动工况
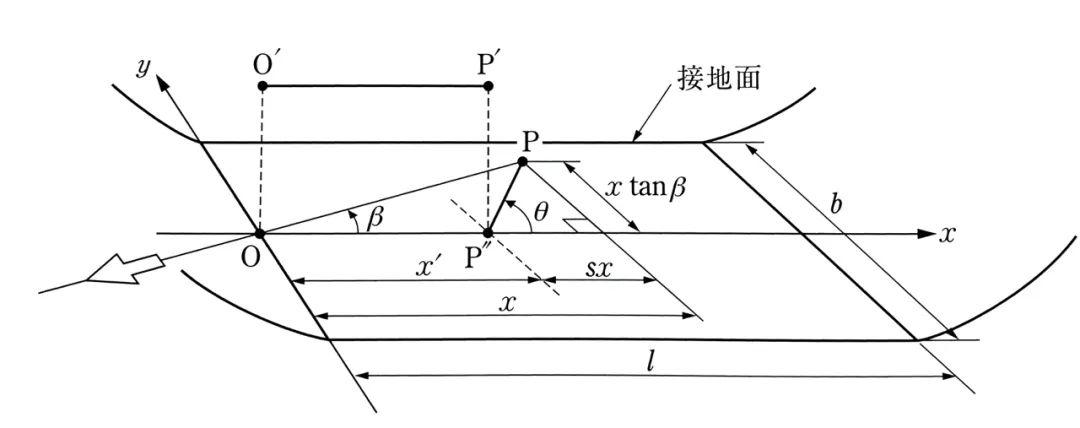
与Fiala之前单纯研究转向侧偏的情况有所区别,在引入纵向运动后,轮胎还会发生纵向滑移。由于刷子模型简化了轮胎的建模,我们只需要考虑胎面橡胶的变形。上图就画出了接地面内轮胎的变形情况。
O‘-P’的轨迹是轮胎胎面基底的运动轨迹,而O-P的轨迹是接地点的移动轨迹。P‘在地面上的投影点为P“,P和P’在x方向上的相对位移可以表示为滑移率s的函数。s可以表达为以下方程:
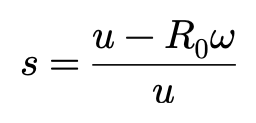
在接地点的附着区,轮胎接地面的单位受力为:
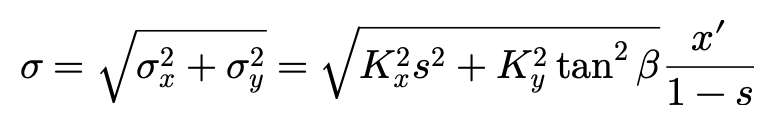
Kx为轮胎胎面橡胶单位长度的纵向刚度,Ky为单位宽度的侧向刚度。
在接地点的滑移区,轮胎接地压力分布与第二小节的方程一致:
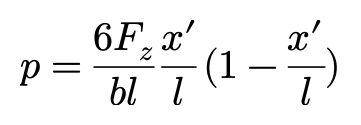
这样,让σ=μp,就可以求解xs‘,即附着区受力曲线和滑移区受力曲线的交界点x坐标。
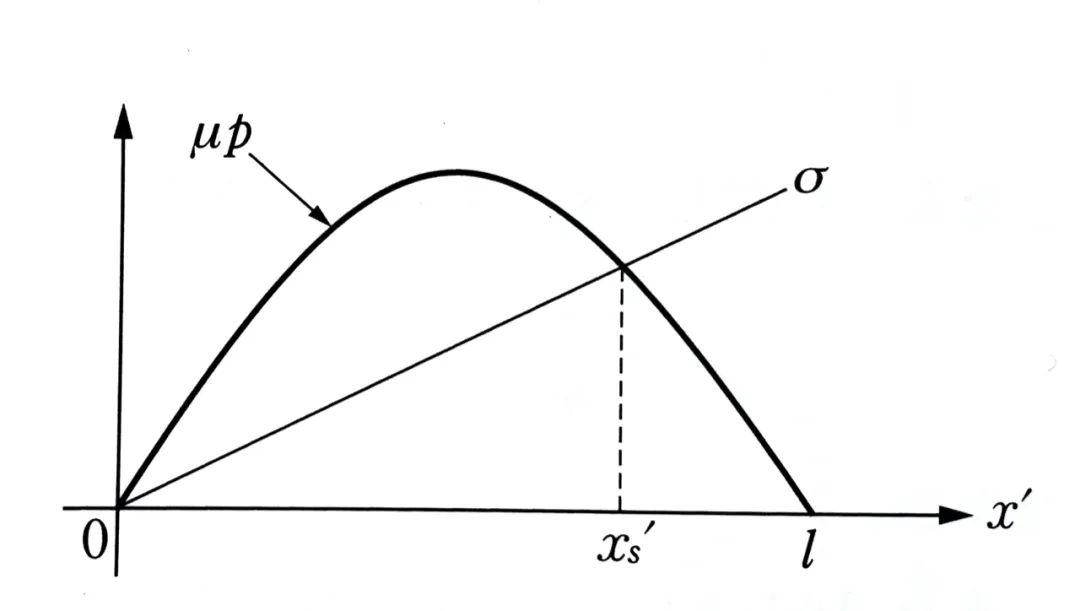
对xs‘进行无量纲化处理并求解,得到ξs:
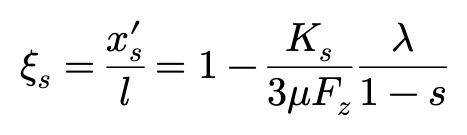
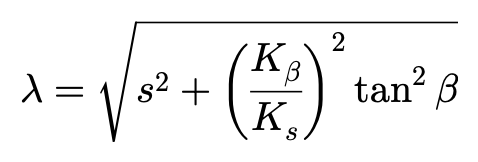
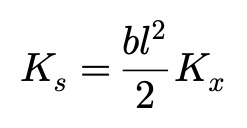
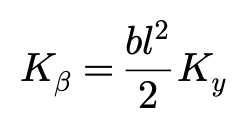
-
当xs‘>0,即ξs>0,则接地区由附着区和滑移区组成;
-
当xs‘=0,即ξs=0,则接地区只存在滑移区
ξs>0时:
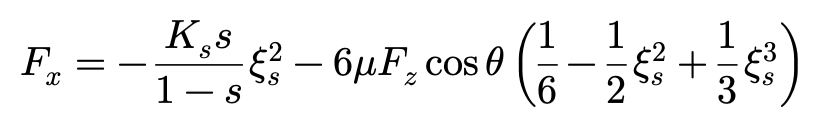
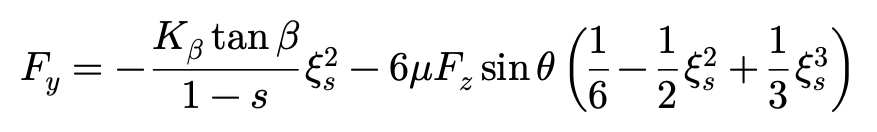
ξs=0时:
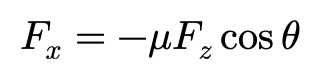
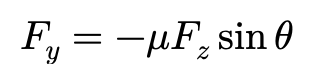
这里假定滑移力的方向θ近似为滑动起点处的滑移方向,即
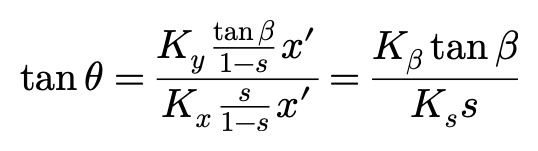
据此,
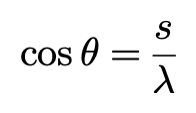
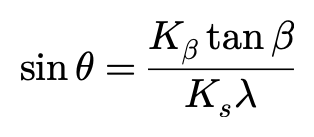
实际上:
Ks相当于侧偏角为零,滑移率趋近于零时单位纵向滑移率所对应的纵向力的总和。
Kβ相当于滑移率为零,侧偏角趋近于零时单位侧偏角对应的侧向力的总和。
而且:
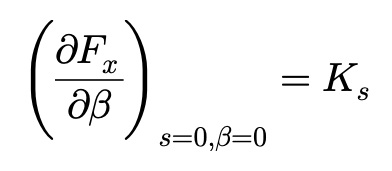 ,
,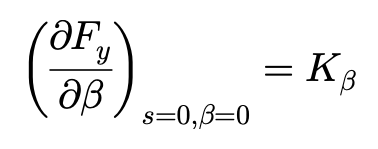
以上Ks和Kβ可以均针对轮胎载荷,通过实验测量来确定。
驱动工况
与制动工况的模型类似,我们可以给出驱动工况的Fx,Fy的表达式:
ξs>0时:
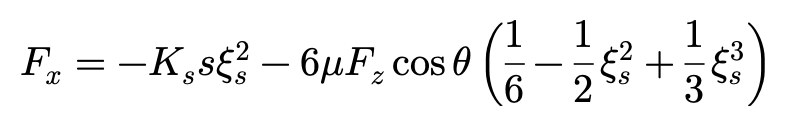
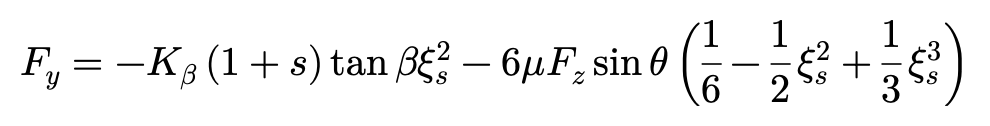
ξs=0时:
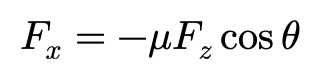
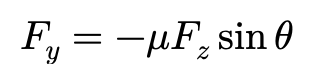
其中,
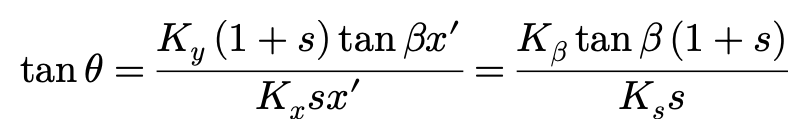
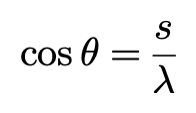
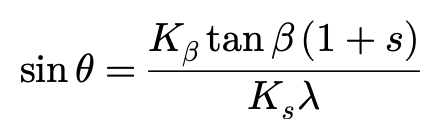
侧向力与纵向力相互作用
侧向力和纵向力关于侧偏角(横すばり角)和纵向滑移率(縦すべり率)的相互作用可以表达为:
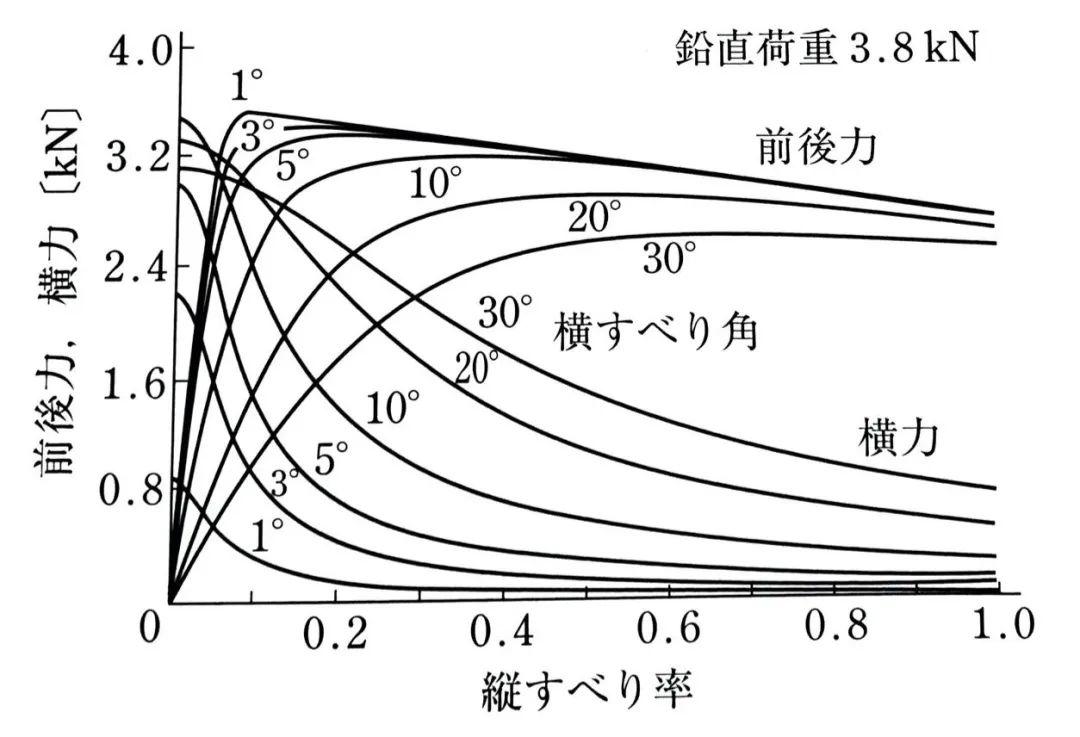
结合制动工况和驱动工况,这两者与侧向力的关系可以表达为:
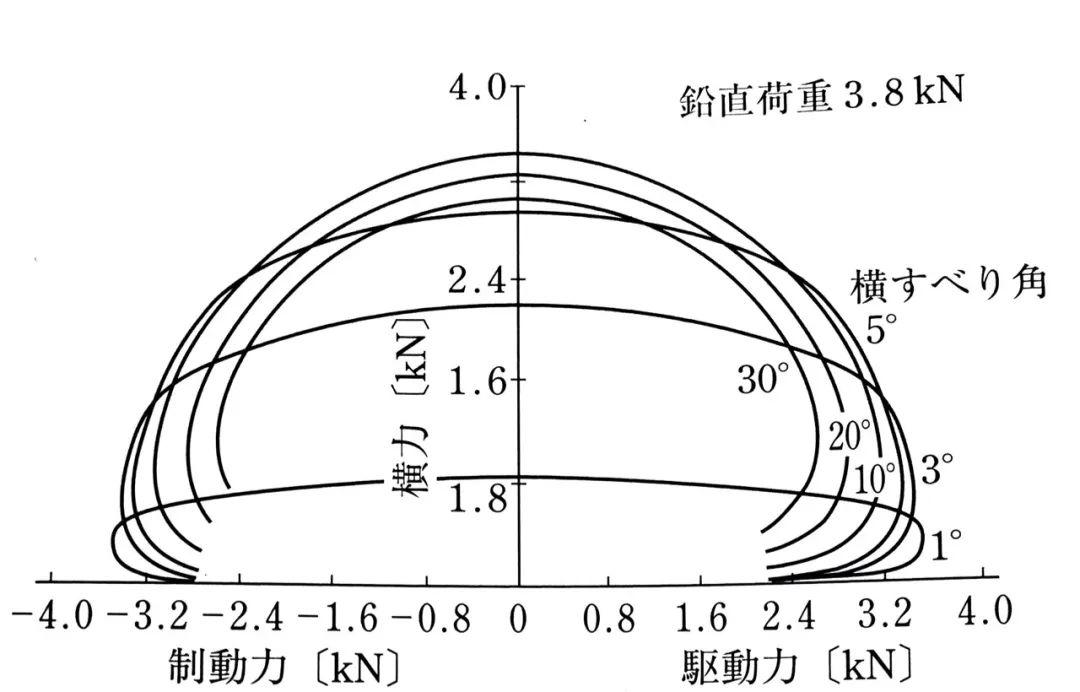
驱动和制动工况下轮胎的回正力矩
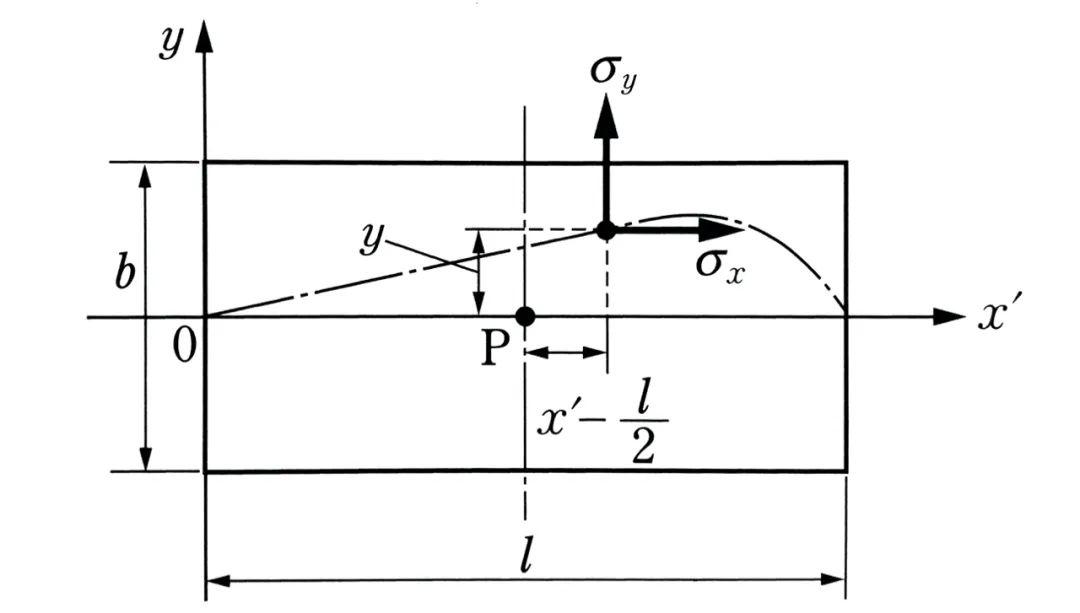
借助复杂的运算,我们可以得到M的积分表达,在这里不再赘述。只写出简化形式:
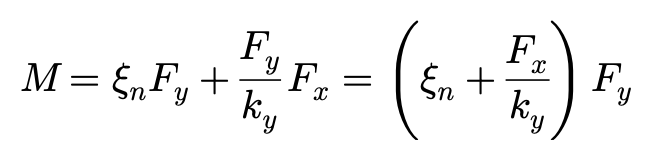
公式中的第一项为侧向力引起的回正力矩;
第二项为纵向力产生的回正力矩——这是由侧向力引起的纵向力作用点偏移Fx/Ky带来的,Ky代表的是轮胎的侧偏刚度。
这里的ξn是轮胎拖距,随侧偏角的增加而减小,相应的轮胎接地面的滑移会增加,并在全滑动的时候趋近于0。
值得注意的是,与轮胎侧向力情形不同,回正力矩在驱动和制动时有很大的差异,且随着侧偏角的变化呈现出相当复杂的规律:
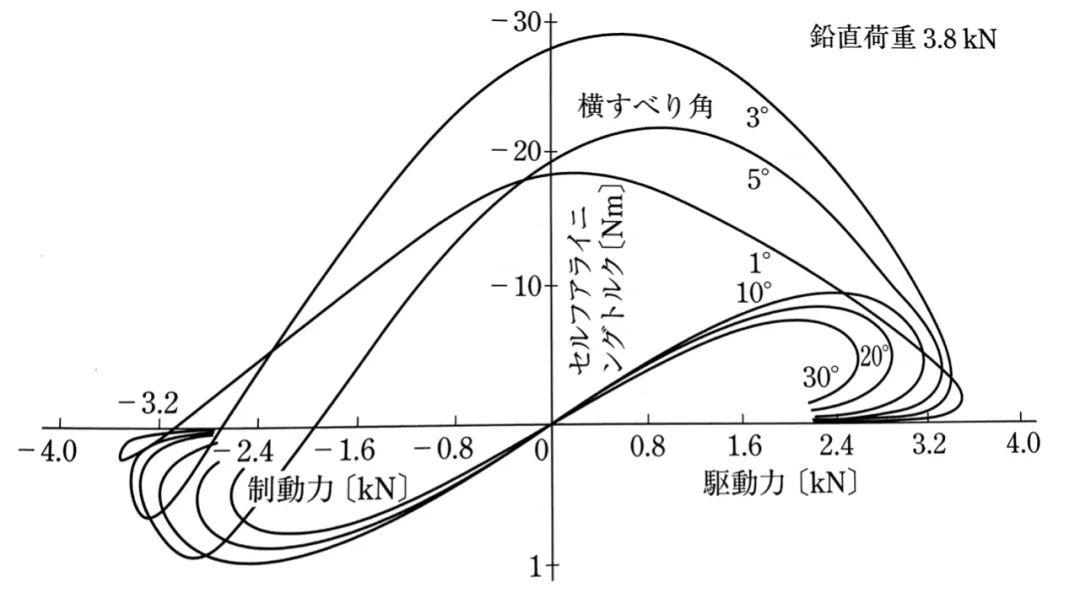
陆
以上关于轮胎力学的讨论的归属于静力学的部分,为了考察侧偏角变化时的瞬时侧向力和回正力矩,我们需要了解轮胎的动态侧偏特性。
Fiala数学模型并不适合用来处理动态的部分,因为模型将复杂到无法进行有效分析。更简化的方式,是限定在小侧偏角范围,利用下文所示宏观轮胎模型考察侧向变形的侧向力和回正力矩的瞬时响应。
侧向力的动态特性
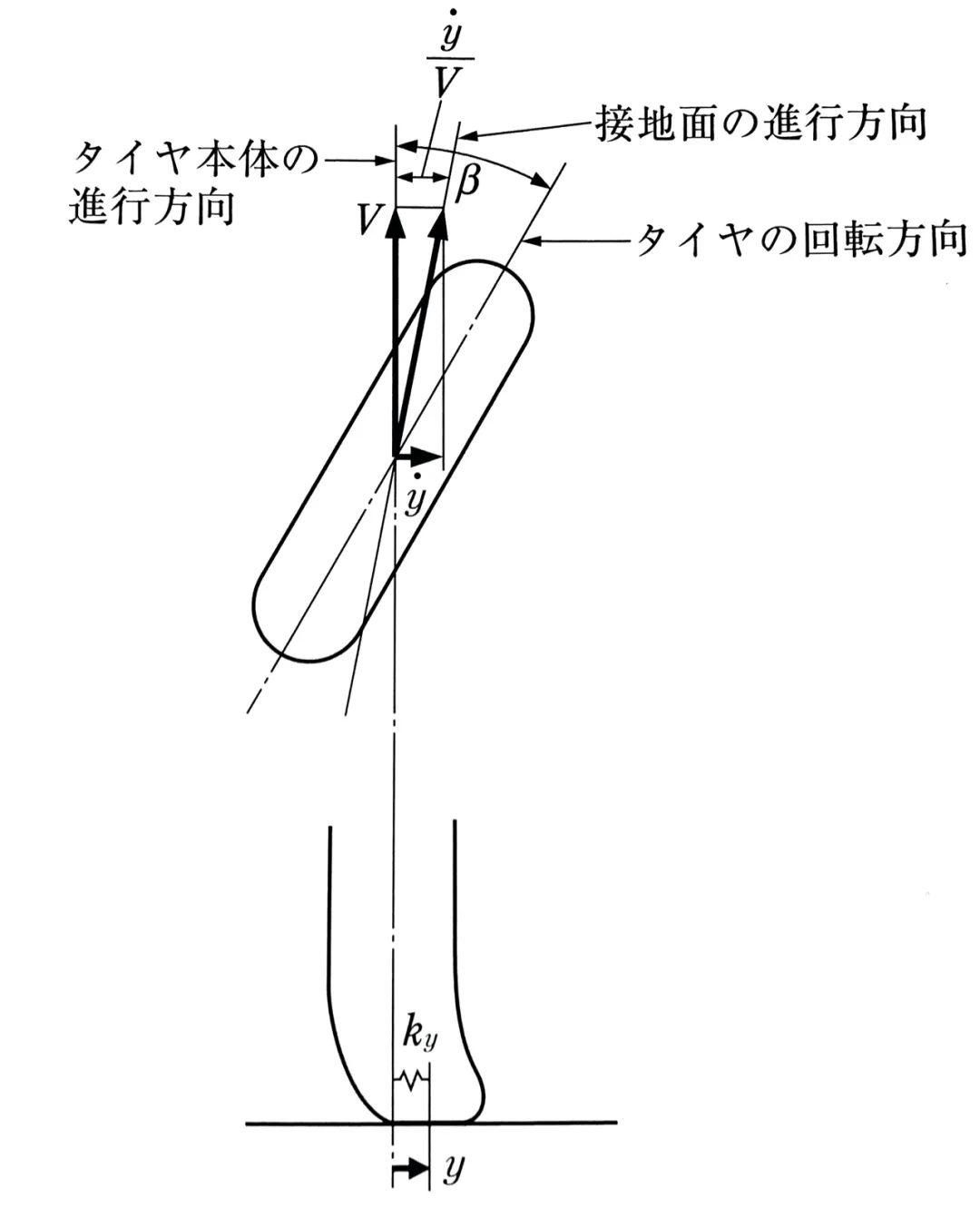
沿轮胎回转方向行驶,突然施加一个侧偏角β时,接地面在侧向产生y的变形,ẏ是接地区的侧向速度,接地区的侧偏角为β-ẏ/V。F为轮胎的侧向力,K为侧偏刚度,则:
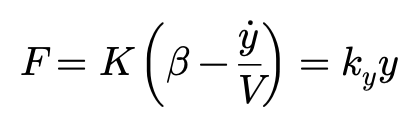
ky为轮胎的侧向刚度。变换消去y,得到:
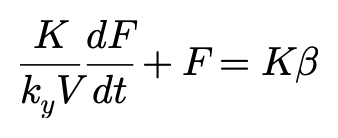
继续做拉普拉斯变换,简化微分方程求解,用侧向力相对于侧偏角的传递函数来表达,得到:
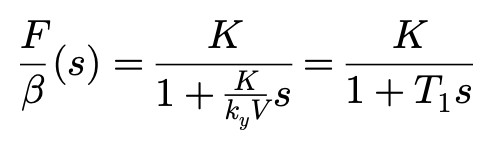
T1简化表达后,所得到的数学形式不是别的,正是一阶延迟环节。再用jω替代s,侧向力的频率响应可以写成:
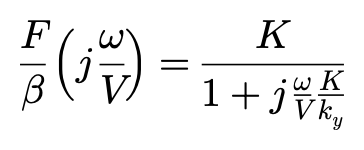
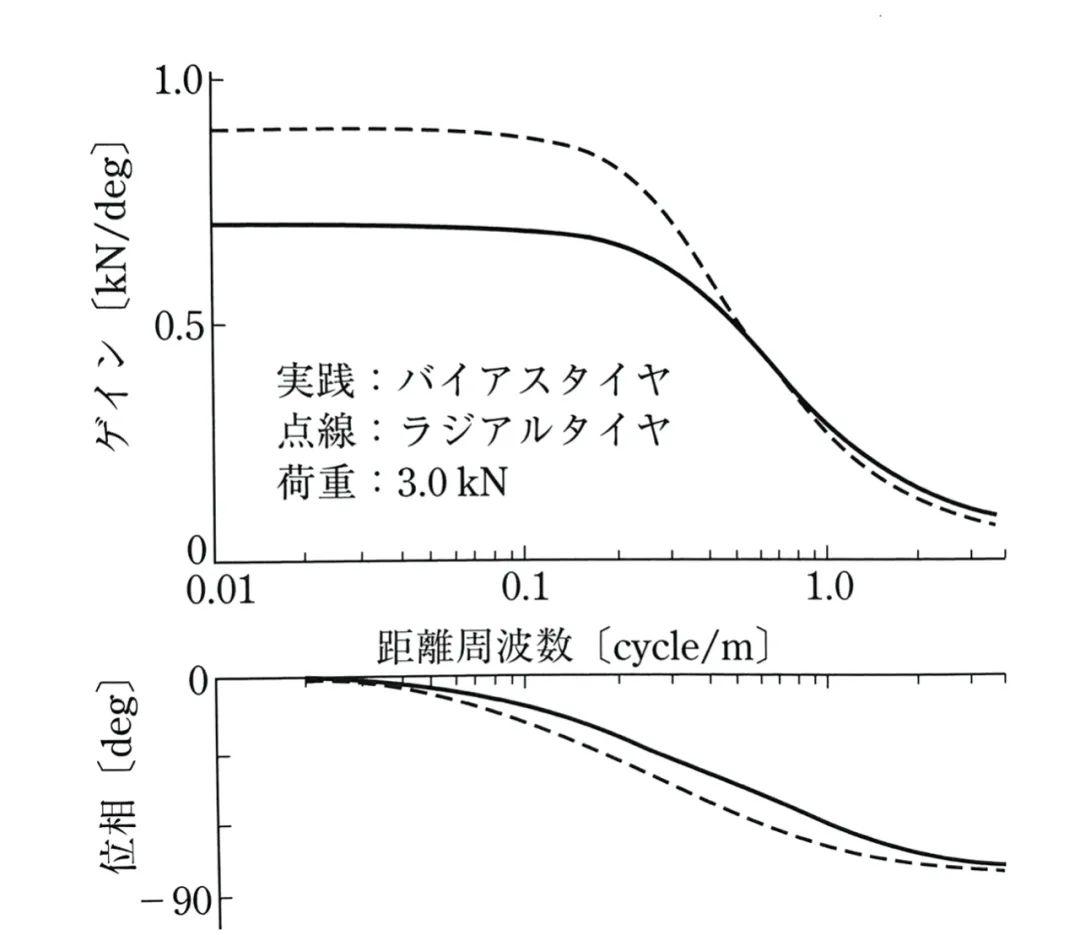
侧向力对侧偏角的频率响应,实线代表斜交轮胎,虚线代表子午线轮胎
回正力矩的动态特性
由侧向力产生的静态回正力矩Ms的响应可以用一阶延迟环节来表达,这里只多乘上了一个轮胎拖距:
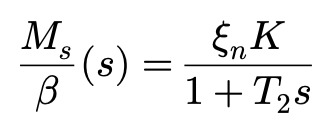
此外,还要考虑轮胎自身突然发生侧偏时,轮胎的扭曲变形——扭曲变形产生的力矩构成瞬时轮胎回正力矩的一部分。可以想象,轮胎的瞬间让扭转角达到侧偏角β,然后,扭转角随轮胎转动而减小,再稳定状态下归零。
这个由轮胎扭转产生的力矩Mt相对于侧偏角的响应,也通过一阶延迟环节来表达:
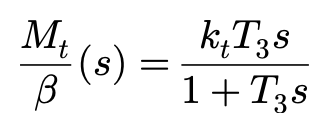
轮胎回正力矩的响应同时包含了Ms和Mt,转换为频率响应后,方程为:
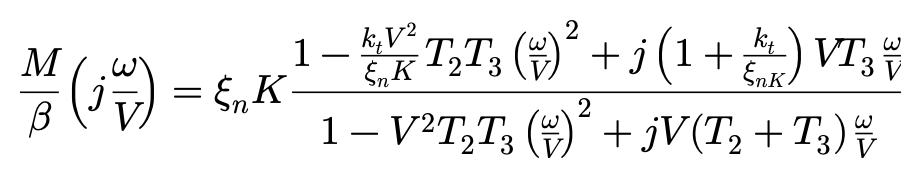
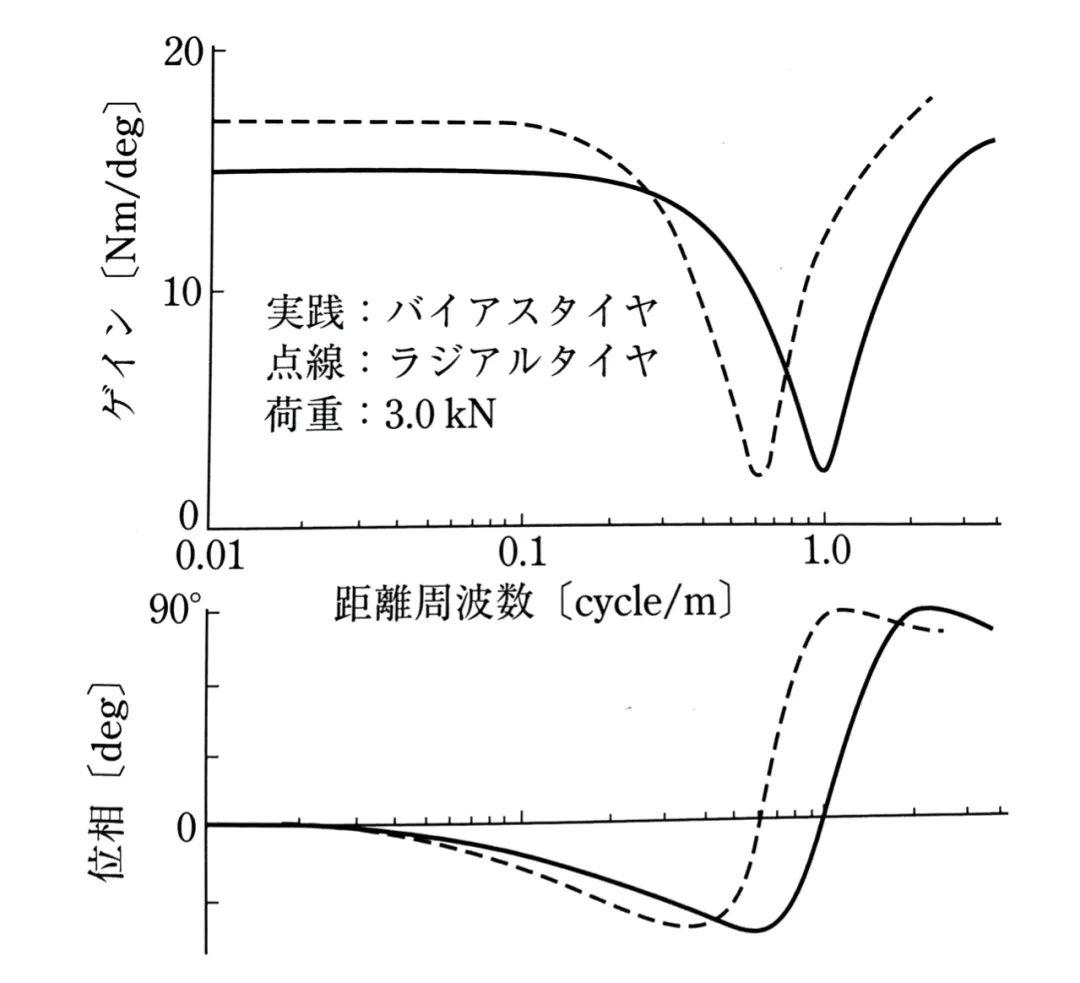
回正力矩相对ω/V的频率响应测量数据也与模型匹配,这间接证实了计算结果的合理性。
完
更多相关文章推荐
-
Part 3 | 无人车安全之战 — AI觉醒的前夜,人类还在沉睡?

本篇文章来源于微信公众号: 几何四驱